Это русский перевод* страницы
http://www.cs.cmu.edu/~bryant/boolean/macgregor.html
 Автора
Автора
Рэндала Э. Брайанта
Основателя Университета
Почетного профессора компьютерных наук
с большим опытом в области электротехники и вычислительной техники
Школа компьютерных наук
Университета Карнеги-Меллона
США
Оригинальная статья
Раскрашивание графа МакГрегора
В апрельском выпуске журнала Scientific American за 1975 год Мартин Гарднер в своей колонке «Математические игры» опубликовал список шести основных математических открытий 1974 года, о которых «по той или иной причине недостаточно сообщалось как научному сообществу, так и общественность в целом ». Одним из них был планарный граф со 110 узлами, приписываемый Уильяму МакГрегору из Ваппингерс-Фоллс, штат Нью-Йорк, который, по его утверждениям, нельзя раскрасить менее чем в 5 цветов, тем самым опровергая пока ещё не доказанное предположение о том, что 4 цветов достаточно для окраски любого планарнго графа. Это не понравилось многим читателям, так это месяц публикации номера. Подробнее об истории можно прочитать здесь .
Вот график, нарисованный в виде карты
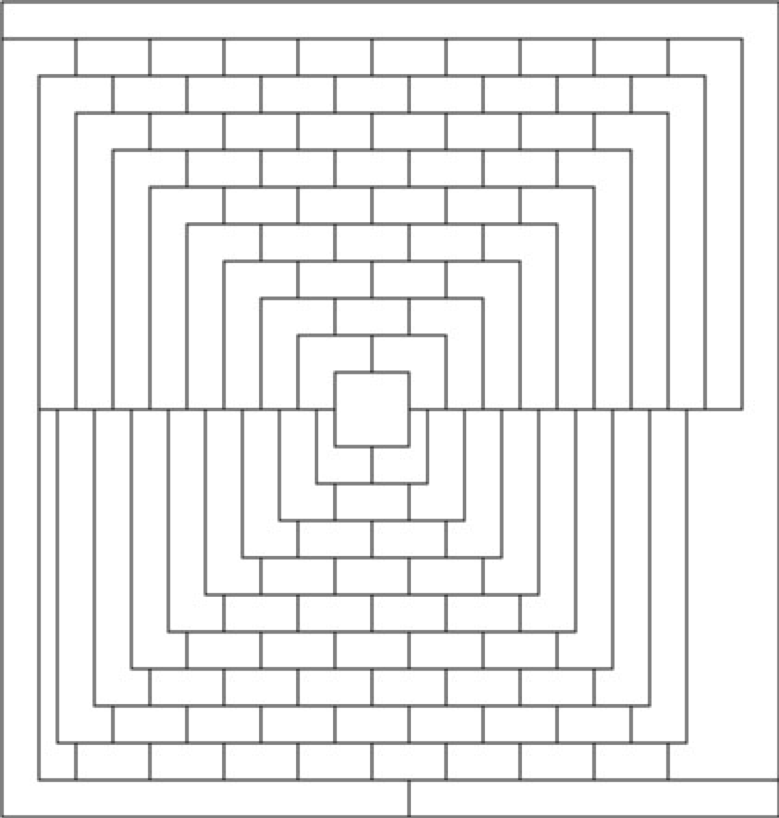
Попытка закодировать возможную окраску этого графа как BDD практически неосуществима. Я предполагаю, что для этого потребуется более одного миллиарда узлов (поскольку минимальный разрез графа имеет ширину 20 узлов, и BDD потребуется экспоненциально кодировать почти все комбинации цветов для этих узлов).
Раскраска графика как задача SAT
С другой стороны, раскраска графа с помощью решателя логической выполнимости (SAT) вполне возможна. Решателю нужно найти только одно возможное решение, поэтому перед ним не стоит сложная задача кодирования всех возможных раскрасок. Вот цвет, созданный решателем ZChaff, проработавшем менее чем одну секунду на портативном компьютере.
 Посмотрите следующее видео на Youtube, показывающее, как продвигается этот поиск: https://youtu.be/0gt503wK7AI
Посмотрите следующее видео на Youtube, показывающее, как продвигается этот поиск: https://youtu.be/0gt503wK7AI
Также можно заставить решатель генерировать «сбалансированную» раскраску, потребовав от него найти решение, используя два цвета (зеленый и синий) 27 раз и два цвета (красный и желтый) 28 раз.

Решатели SAT также могут использоваться для решения задач оптимизации, выполняя серию вызовов решателей для выполнения двоичного поиска по целевой функции. Если мы попросим решающую программу найти раскраску, которая сначала минимизирует количество узлов, окрашенных в зеленый цвет, а затем минимизирует число, окрашенное в синий цвет, а затем в красный, мы получим раскраску всего из 7 зеленых узлов, 34 синих и красных и 35 желтых.

На основании дальнейших экспериментов можно констатировать, что до назначения цветов это решение обладает уникальными свойствами:
- Это единственная окраска, в которой один цвет используется не более 7 раз.
- Это единственная окраска, в которой один цвет используется не менее 35 раз.
_______________________________________________________________________________________________________________
Последнее изменение: среда, 12 мая, 10:19:05 EDT 2010
![]() © 2020.
© 2020.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License (https://creativecommons.org/licenses/by-sa/4.0/)**.
*Уполномоченный русский перевод
Публикация 8 октября 2020
Текущая версия:
https://thesisowl.com/2020-10-08-macgregor-1t/
Последняя версия:
https://thesisowl.com/2020-10-08-macgregor-2t/
Оригинальная версия (на английском языке):
http://www.cs.cmu.edu/~bryant/boolean/macgregor.html
Организатор перевода:
ThesisOwl,
Украина, Киев, 01014,
бул. Леси Украинки, 26, 3 этаж
Сайт: https://thesisowl.com
Редакторская правка перевода
EuroWay
Украина, Киев, 03035, Соломенская площадь, 2, 6 этаж
Координатор перевода
Девид Диаз (e-mail: [email protected])
Настоящий документ является авторизованным переводом документа Массачусетского университета г.Амхерст(https://people.umass.edu ). Публикация этого перевода производится в соответствии с этапами, описанными в правилах подготовки авторизованных переводов (Policy for W3C Authorized Translations). Во всех спорных случаях основной считается оригинальная версия данного документа на английском языке.
**Creative Commons
Мы публикуем этот перевод и звуковой файл, его воспроизводящий для людей с проблемами зрения, как производные документы по лицензии Creative Commons. Вы можете использовать наши материалы и развивать работу в некоммерческих или коммерческих целях при условии, что вы выполните оригинальную публикацию и включите обратную ссылку на thesisowl.com (https://thesisowl.com/2020-10-08-macgregor-2t/).
Это официальная лицензия Creative Commons:

Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)
Вы можете:
Share – копировать и распространять материал на любом носителе и любом формате.
Adapt – ремикшировать, преобразовывать и дополнять материал для любых целей, даже в коммерческих целях.
На следующих условиях:
Attribution – вы должны указать соответствующую отметку, предоставить ссылку на лицензию и указать, были ли внесены изменения. Вы можете сделать это любым разумным способом, но не любым способом, который предполагает, что лицензиар одобряет вас или ваше использование.
ShareAlike – если вы уменьшаете, трансформируете или дополняете материал, вы должны распространять свои материалы по той же лицензии, что и оригинал.
Детали лицензии: https://creativecommons.org/licenses/by-sa/4.0/
КАК СОСЛАТЬСЯ НА ЭТУ ПУБЛИКАЦИЮ (HOW TO CITE THIS PUBLICATION):
Якорь (ancor) – ThesisOwl
URL – https://thesisowl.com/2020-10-08-macgregor-2t/
Пример (example) – ThesisOwl