Интересные задачи с картой
Вот несколько переводов этой страницы на другие языки:
- Наболгарском языке любезно предоставлено Рико Низзо.
- Нафинском языке любезно предоставлено Эльзой Янссон .
- Нафранцузском языке любезно предоставлено Дэвидом Варделлом .
- Нанемецком языке любезно предоставлено Филипом Эггером.
- Наиндонезийском любезно предоставлено Джорданом Силаеном
- На итальянском любезно предоставлено Emfurn .
- Намакедонском любезно предоставлено Еленой Симски.
- Напольском языке любезно предоставлено Мареком Муравски.
- Нарумынском языке любезно предоставлено Иринией Василеску.
- НаТамале любезно предоставлено Vikatan.com .
Дон Кнут работает над четвертым томом « Искусства компьютерного программирования » . Одна из глав посвящена диаграммам двоичных решений и их приложениям – теме, которая мне очень интересна. Кнут показывает, что множество интересных задач с графами можно закодировать в виде булевых формул, а производный BDD представляет все возможные решения проблемы. Часто существует какой-то критерий оптимизации, и довольно легко извлечь «лучшее» решение из BDD с помощью простого алгоритма динамического программирования.
Здесь мы показываем несколько примеров, используя граф, представляющий 48 смежных состояний, с узлом для каждого состояния и границей между двумя состояниями, если они имеют общую границу. Для каждой карты, если вы нажмете на изображение, вы попадете в исходный документ в формате SVG . Вот график, на котором расположены узлы в столицах штатов:
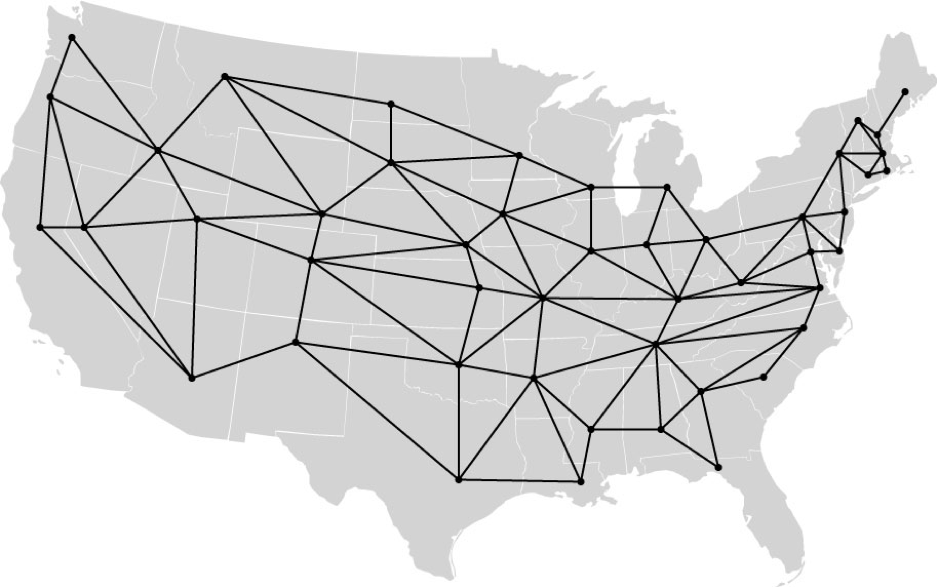
Столичные туры
Предположим, вы хотите посетить столицу 48 штатов с требованием, чтобы вы проходили через каждый штат только один раз. (Другими словами, вы хотите найти Гамильтонов путь на графике.) Как видно из приведенной выше карты, если вы будете следовать наиболее прямому маршруту между столицами штатов, вы часто будете проходить через другой штат или, в случае по пути из Лансинга, штат Мичиган, в Мэдисон, штат Висконсин, вы проедете через озеро Мичиган. Вместо этого вам следует выбрать кратчайший маршрут движения, который не выходит за пределы двух штатов на каждом отрезке пути. Назовем такой маршрут Столичным Туром . Вот схема допустимых маршрутов между состояниями:
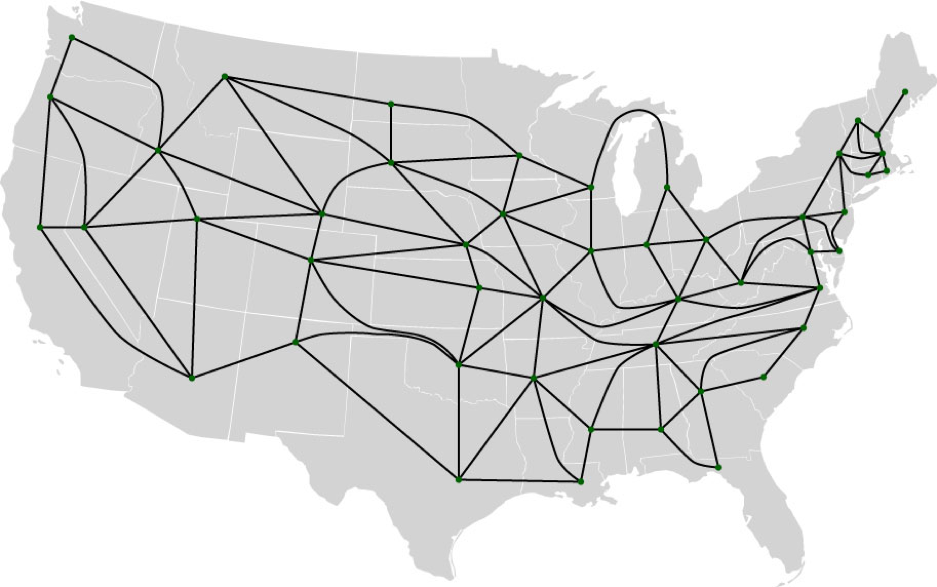
Основываясь на простом анализе и усилиях Кнута, мы можем сказать следующее:
- Все туры должны начинаться или заканчиваться в штате Мэн, поскольку у штата Мэн только один сосед. Мы будем использовать штат Мэн в качестве отправной точки.
- Все туры должны заканчиваться за пределами Нью-Йорка, поскольку это точка сочленения.
- Всего насчитывается 68 656 026 различных столичных туров.
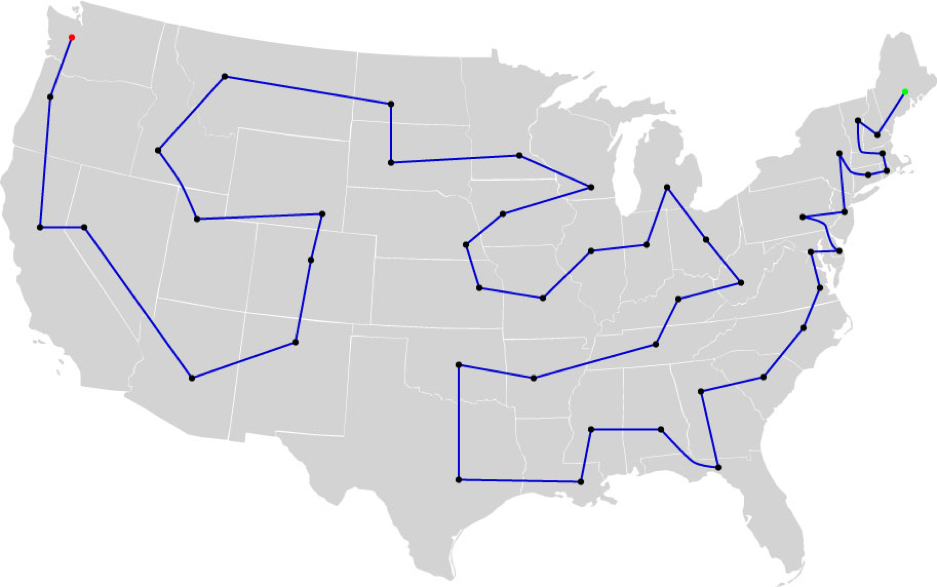
Вот самый короткий тур по столицам общей протяжённостью 11 698 миль:
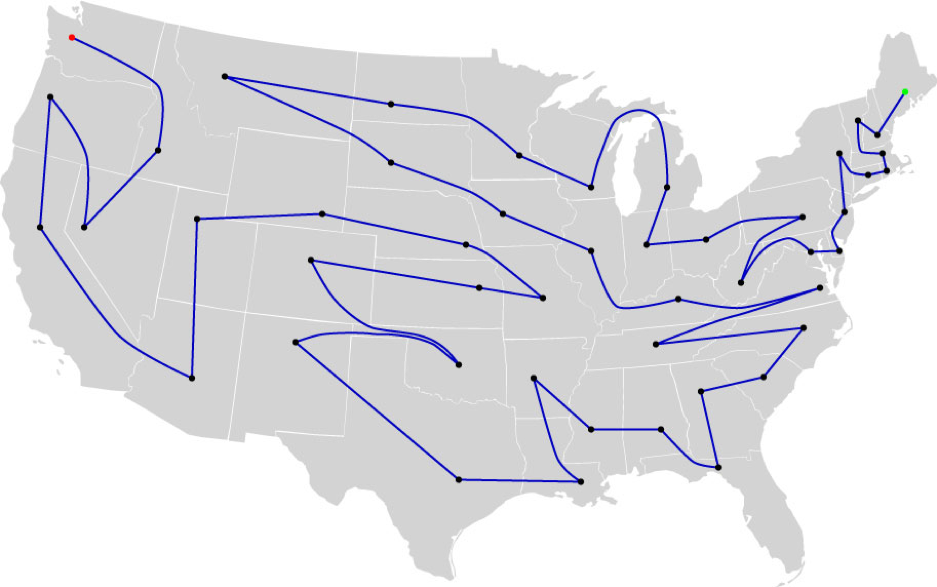
Вот самый длинный тур по столицам общей протяжённостью 18 040 миль:
Раскраска графика
Еще один интересный класс задач – раскрашивание карты. Правило состоит в том, что никакие два соседних состояния не могут иметь одинаковый цвет. Знаменитая теорема о четырех цветах утверждает, что любой плоский граф можно раскрасить не более чем в четыре цвета.
Поскольку BDD кодирует все возможные решения булевой формулы, мы можем легко вычислить, сколько существует решений. Для раскраски графа мы корректируем наши подсчёты, чтобы устранить симметрии из-за произвольного назначения значений цвета (4! Симметричных случая для 4-раскраски).
Для раскраски 48 смежных состояний существует 533 816 322 048 возможных раскрасок. (Это 1/2 числа, указанного Кнутом, поскольку на его карте Вашингтон, округ Колумбия, указан как 49-й «штат», и ему может быть присвоен любой из двух цветов, не используемых для Мэриленда и Вирджинии.) Вот несколько интересных примеров. специальные расцветки:
- Сбалансированная окраска, в которой каждый цвет используется ровно для 12 состояний. Всего таких окрасок 12 554 677 864, что составляет удивительно высокие 2,4% от всех возможных окрасок.
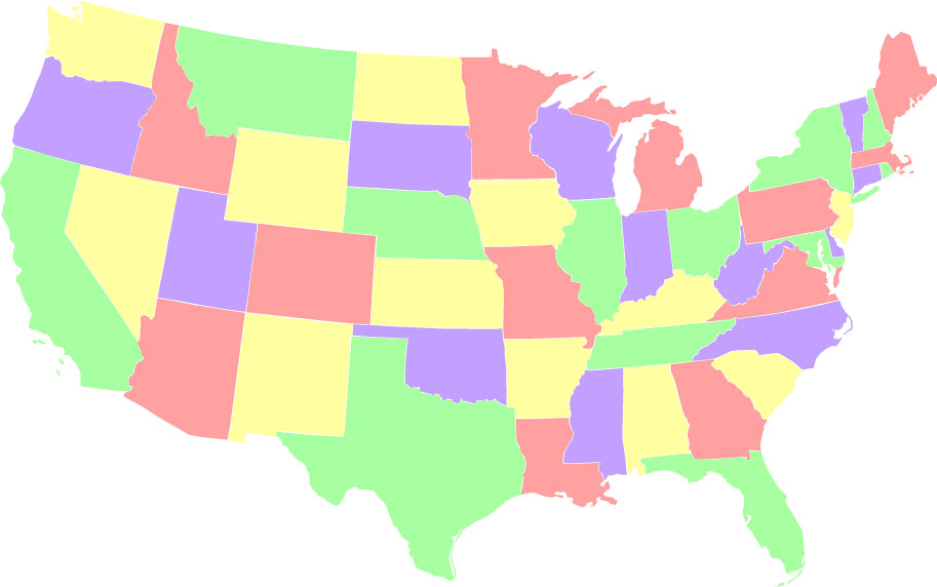
- Несбалансированная окраска, при которой один из цветов (зеленый) используется как можно меньше (2 состояния). Есть всего 288 способов раскрасить карту, чтобы один цвет использовался дважды.
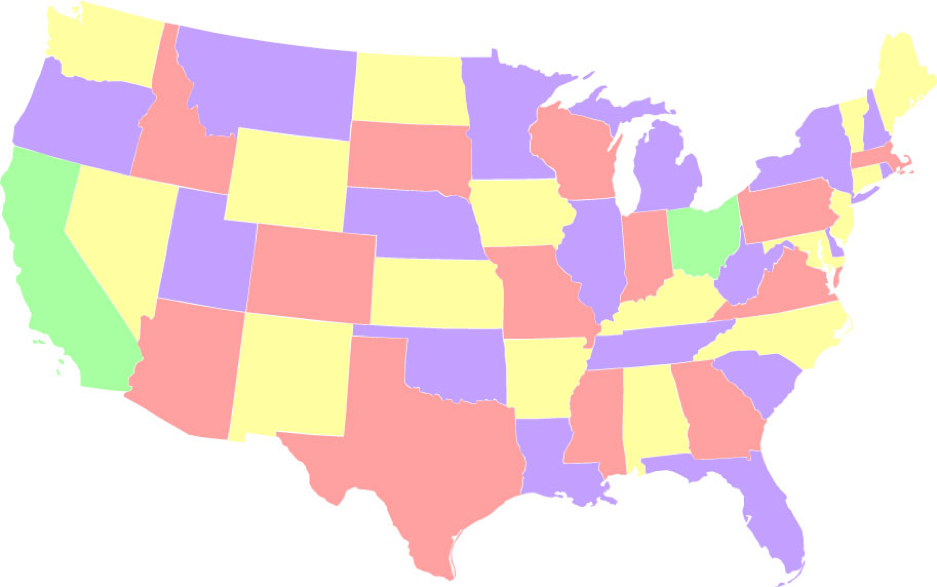
- Несбалансированная окраска, при которой максимально используется один из цветов (желтый) (18 состояний). Существует 71 002 368 способов раскрасить карту, чтобы один цвет использовался 18 раз.
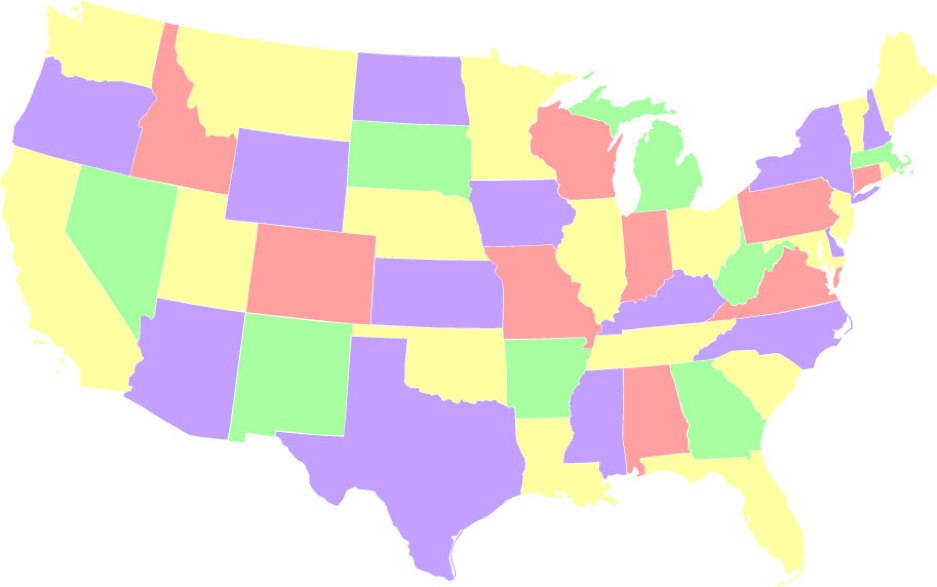
- Сочетание обоих. Раскрашивание с использованием цветов 2, 13, 15 и 18 раз. Эта последовательность: 1) слева направо использует каждый цвет последовательно наименьшее возможное количество раз и 2) справа налево использует каждый цвет последовательно максимально возможное число раз. Всего существует 24 таких решения.
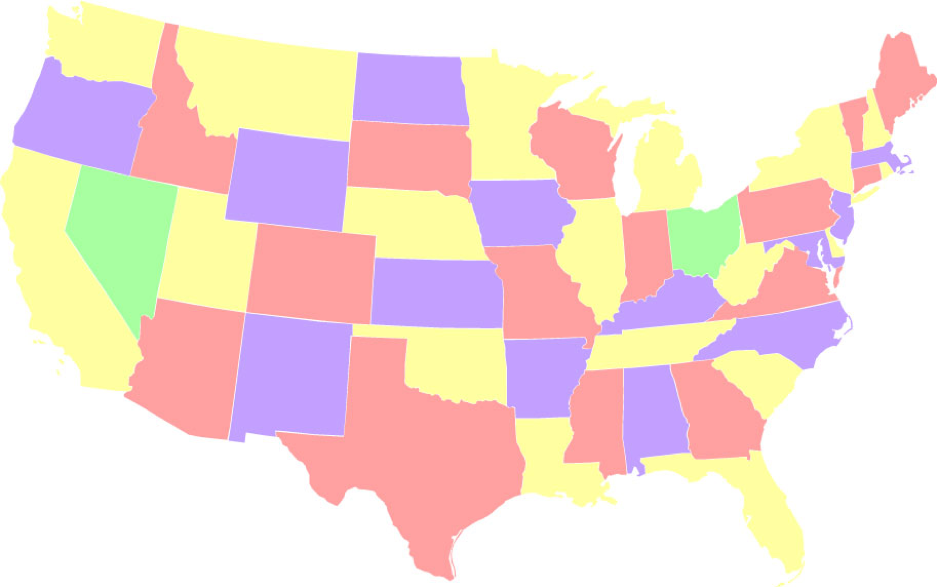
С точки зрения программ раскраски графиков карта 48 штатов США довольно проста. Более сложную карту можно найти на веб-странице Графика МакГрегора .
_______________________________________________________________________________________________________________
Последнее изменение: Вт, 19 января, 07:48:18 EST 2010