Цікаві проблеми з картою
Ось декілька перекладів цієї сторінки іншими мовами:
Болгарською мовою надано Ріко Ніццо.
Фінською мовою – Ельза Янссон .
Французькою люб’язністю надав Девід Уорделл .
Німецькою ввічливістю Філіпа Еггера.
Індонезійською з люб’язністю надано Джорданом Сілаєном
З італійської ввічливості Емфурн .
По-македонськи люб’язно надано Оленою Сімскі.
По-польськи люб’язно надано Мареком Муравським.
Румунською мовою надано Ірінією Василеску.
На тамалі надано Vikatan
Дон Кнут працює над 4 томом « Мистецтва комп’ютерного програмування» . Один із розділів стосується двійкових схем прийняття рішень та їх застосувань – тема, яка мені здається дуже цікавою. Кнут показує, що безліч цікавих графічних задач можна закодувати як булеві формули, а отриманий BDD представляє всі можливі рішення проблеми. Часто існує якийсь критерій оптимізації, і досить просто витягти «найкраще» рішення з BDD за допомогою простого алгоритму динамічного програмування.
Тут ми покажемо кілька прикладів, використовуючи графік, що представляє 48 суміжних станів, з вузлом для кожного стану та ребром між двома станами, якщо вони мають спільну межу. Якщо натиснути на зображення, для кожної з карт ви отримаєте вихідний документ у форматі SVG . Ось графік розташування вузлів у столицях штатів:
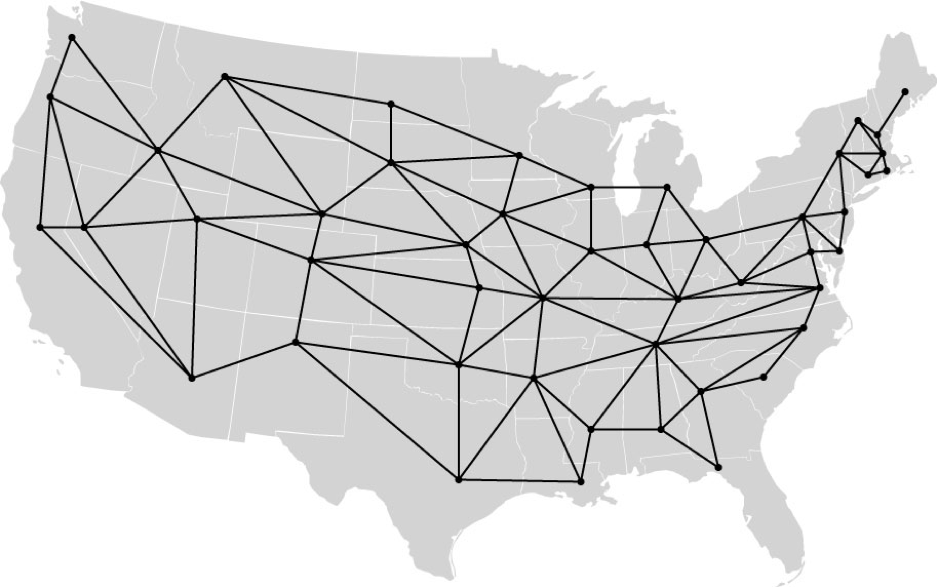
Столичні тури
Припустимо, ви хочете відвідати столицю 48 штату з вимогою проїхати через кожну державу лише один раз. (Іншими словами, ви хочете знайти гамільтонівський шлях на графіку.) Як ви можете бачити з наведеної вище карти, якщо ви будете слідувати найбільш прямому шляху між столицями штатів, ви часто проходите через інший штат, або у випадку ідучи від Ленсінга, штат Мічиган до Медісона, штат Вісконсін, ви проїдете через озеро Мічиган. Натомість вам слід пройти найкоротший маршрут водіння, який залишається в межах двох штатів на кожному етапі подорожі. Давайте назвемо такий маршрут столичним туром . Ось схема допустимих маршрутів між штатами:
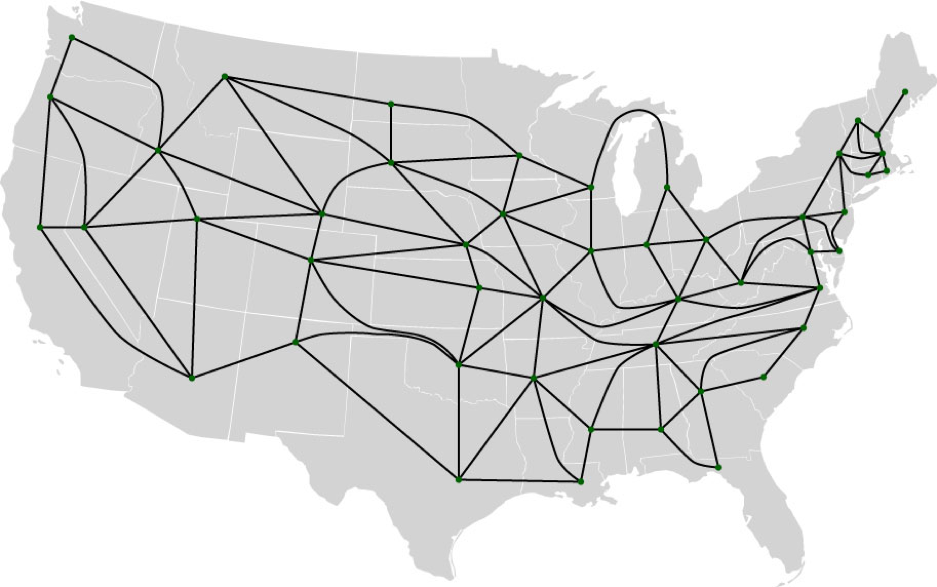
На основі простого аналізу, плюс зусиль Кнута, можна сказати наступне:
- Усі тури повинні починатися або закінчуватися в штаті Мен, оскільки в штаті Мен є лише один сусід. Ми використаємо Мен як вихідну точку.
- Усі тури повинні закінчуватися за межами Нью-Йорка, оскільки це пункт артикуляції.
- Загалом є 68 656 026 різних столичних турів.
Ось найкоротший столичний тур на загальну суму 11 698 миль:
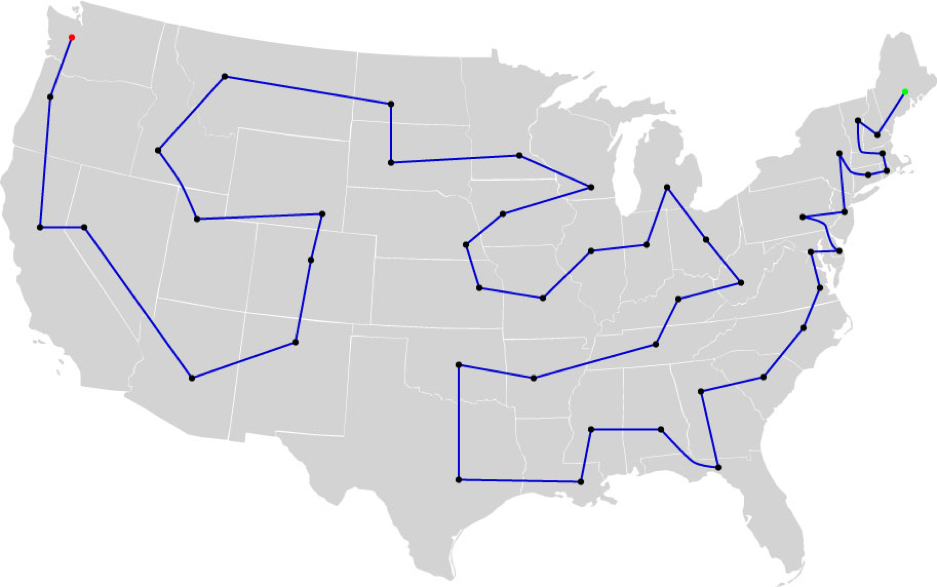
Ось найдовший столичний тур на загальну суму 18 040 миль:
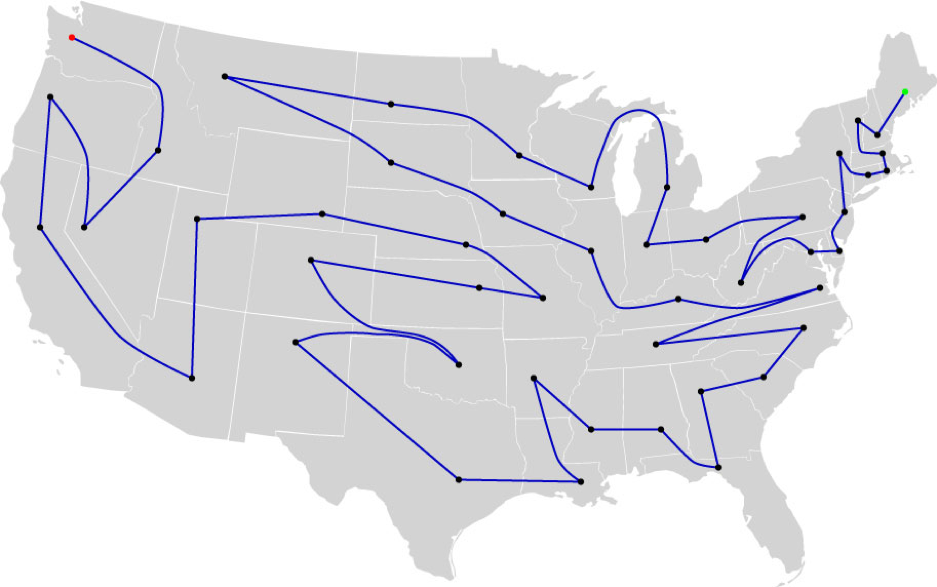
Графічне забарвлення
Інший цікавий клас задач передбачає розфарбовування карти. Правило полягає в тому, що жоден із двох сусідніх станів не може мати однаковий колір. Відома теорема чотирьох кольорів стверджує, що будь-який площинний графік може бути забарвлений щонайбільше чотирма кольорами.
Оскільки BDD кодує всі можливі рішення до булевої формули, ми можемо легко розрахувати, скільки існує рішень. Для розфарбовування графіків ми коригуємо нашу кількість, щоб усунути симетрії через довільне присвоєння значень кольору (4! Симетричні випадки для 4-забарвлення).
Для фарбування сусідніх 48 штатів існує 533 816 322 048 можливих забарвлень. (Це 1/2 числа, про яку повідомив Кнут, оскільки його карта включає Вашингтон, округ Колумбія, як 49-й “штат”, і їй може бути присвоєний будь-який із двох кольорів, які не використовуються для штатів Меріленд та Вірджинія.) Ось кілька цікавих прикладів спеціальні барвники:
- Збалансоване забарвлення, при якому кожен колір використовується рівно 12 станів. Налічується 12 554 677 864 таких забарвлень, що є напрочуд високим 2,4% від усіх можливих забарвлень.
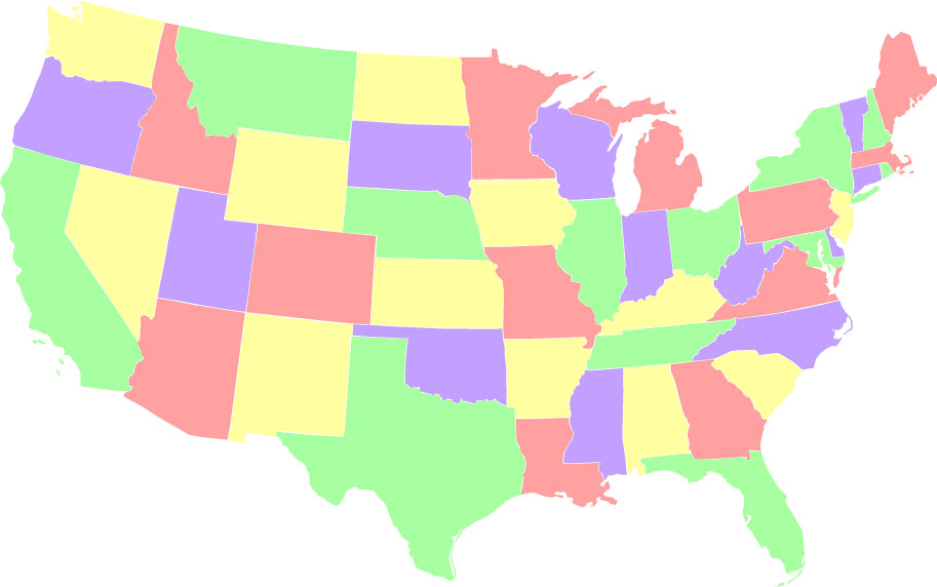
- Незбалансоване забарвлення, при якому один із кольорів (зелений) використовується якомога менше (2 стани). Є лише 288 способів розфарбувати карту таким чином, щоб один колір використовувався лише двічі.
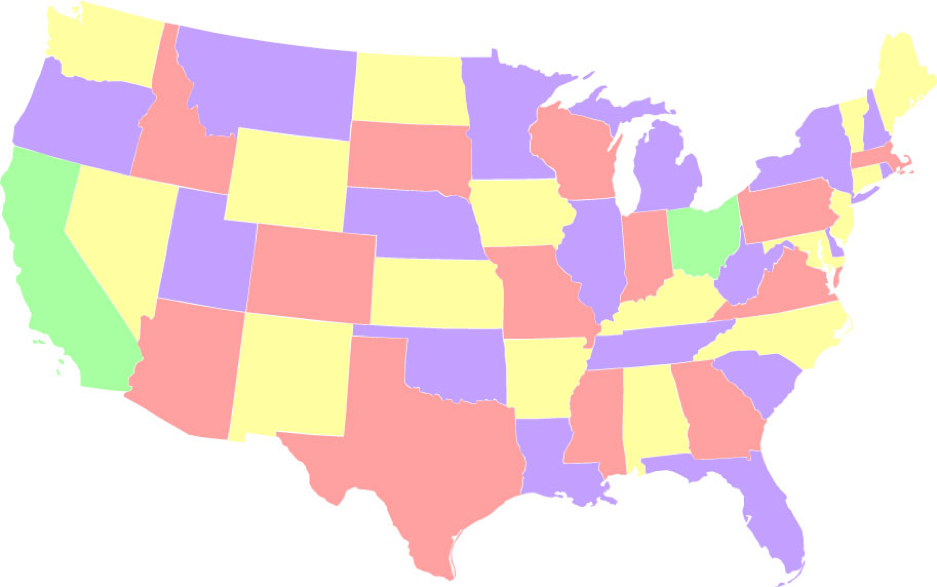
- Незбалансоване забарвлення, при якому якомога більше використовується один із кольорів (жовтий) (18 станів). Існує 71 002 368 способів розфарбувати карту таким чином, щоб один колір використовувався 18 разів.
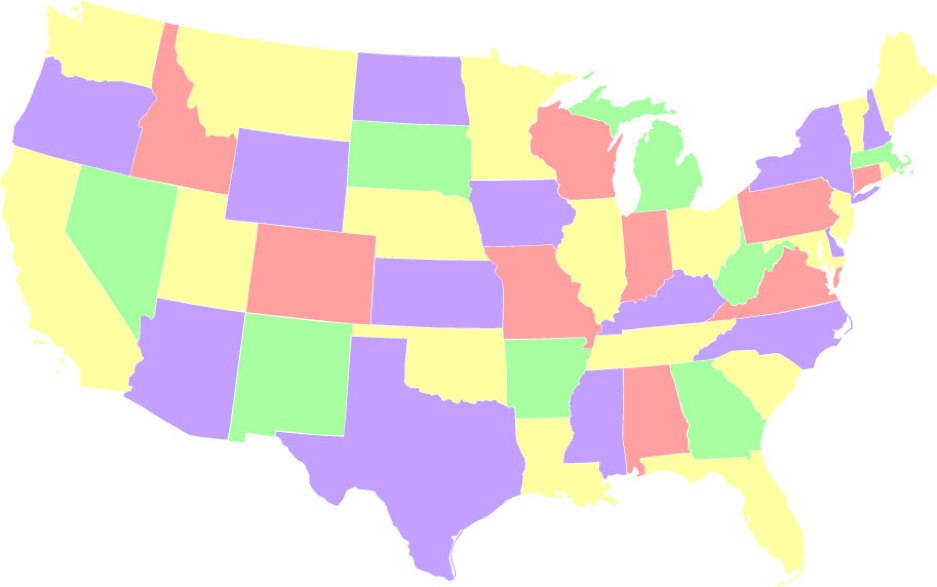
- Поєднуючи обидва. Розмальовки, використовуючи кольори 2, 13, 15 та 18 разів. Ця послідовність 1) зліва направо, використовує кожен колір послідовно найменшу можливу кількість разів, і 2) справа наліво, використовує кожен колір послідовно максимально можливу кількість разів. Таких рішень 24.
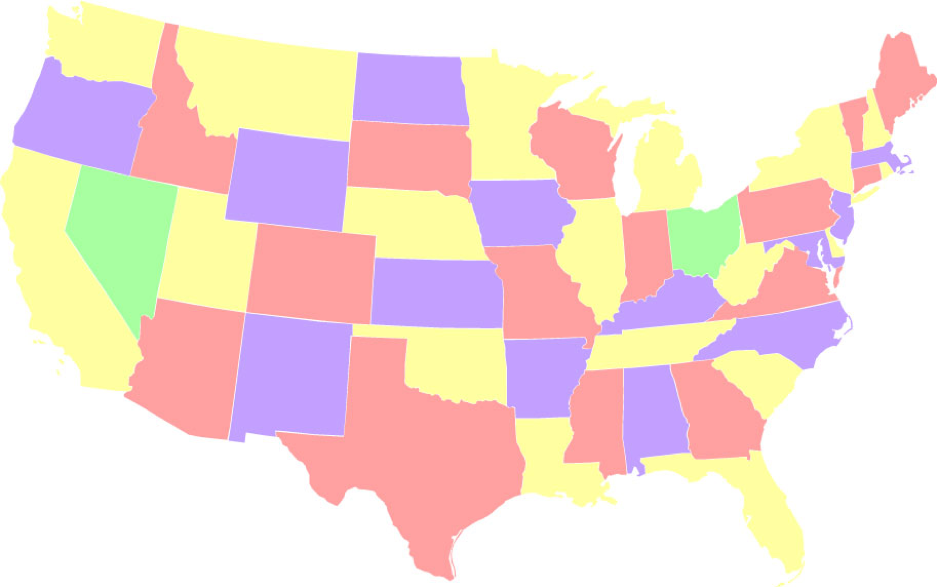
З точки зору програм забарвлення графіків, карта 48 штатів США є досить простою. Для більш складної карти див. Веб-сторінку на Графіку Макгрегора .
______________________________________________________________________________________________________________
Останнє редагування: вівторок, 19 січня 07:48:18 за EST, 2010