Алгоритмы и их анализ
Педагогическое введение
В.В.Сетзер и Ф.Х. Карвалхейро,
кафедра компьютерных наук, Университет Сан-Паулу
www.ime.usp.br/~vwsetzer
Перевод выполнен из [1] VWS,
английская редакция CMTolman – Версия 1.4,
14 марта 2009 г.
- Введение
Алгоритмы существуют с древних времён. Выполнение суммы двух чисел с большим количеством цифр относиться к алгоритму; хорошо известный «алгоритм Евклида» для вычисления максимального общего делителя, если его автора можно считать первооткрывателем, то он датируется 3 веком до нашей эры.
Сегодня понятие и область применения алгоритмов стали абсолютно необходимыми, потому что каждая «работающая» компьютерная программа, то есть дающая ожидаемые результаты, вероятно, является описанием алгоритма. (Если читатель находит «вероятно» немного странным, ему или ей, вероятно, нужно лучше понять, что такое алгоритмы и что такое программы…) Кроме того, если кто-то хочет разработать программу для компьютера, правильный способ сделать это было бы сначала искать наиболее адекватный метод решения задачи, задавая это решение в виде алгоритма, а затем выражая его на каком-либо компьютерном языке для вставки в компьютер с последующей его (автоматической) интерпретацией или переводом на машинный язык и его выполнение.
С образовательной точки зрения нам кажется существенным, что учить тому, что «программирование компьютера» не означает давать машине какие-то команды, выраженные в синтаксисе какого-либо языка программирования, модифицировать и затем переставлять их до тех пор, пока не будет получен ожидаемый результат, как это происходит с электронной (видео) игрой. Суть программирования и вычислительной техники, предмета, который действительно должен заинтересовать студентов в этой области, заключается в разработке и анализе алгоритмов.
В данной статье представлена учебная деятельность, основанная на понятии алгоритмов и анализе их сложности. Исходя из нашего опыта, мы считаем его адекватным для старших классов средней школы. Его продолжительность составляет около 3 часов. Это не требует от студентов предыдущего опыта работы с компьютером. В нем используется физкультурно-педагогический материал, представляющий задачу с числами в виде соревновательной ручной игры. Учащиеся решают задачу в группах, имея разумное пространство для проявления своего творчества. Затем они сравнивают различные решения, полученные разными группами. Далее преподаватель делает абстракцию понятий, связанных с решением предложенной задачи, и предлагает более сложное и эффективное решение. Затем он или она вводит расширенные концепции, такие как правильность и сложность алгоритма, понятие оптимального алгоритма и неразрешимость некоторых проблем. Все это делается без какой-либо связи с компьютером, поэтому наличие таких машин не обязательно для введения концептуальных понятий вычислений и программирования. С другой стороны, если компьютеры доступны, наш метод может служить для внедрения практического программирования.
- Предлагаемая проблема
Для введения искомых идей мы выбрали задачу сортировки n чисел.
2.1. Заявление
В качестве педагогической дидактики преподаватель сообщает студентам, что его менеджер поставил перед ним следующую задачу:
«Вот доска с карманами, пронумерованными от 1 до 8 (рис. 1). Внутри каждого кармана полоска картона, на которой написано натуральное число. Вы должны переставить полоски так, чтобы они располагались в порядке возрастания от слева направо по следующим правилам:
П1. Можно поднять полоску из отделения, чтобы проверить её содержимое, то есть число, написанное на ней.

Рис. 1
П2. Если полоска находится внутри кармана со скрытым номером, она считается неизвестной. Вы не должны запоминать содержимое карманов.
П3. Одновременно можно поднять не более 2 планок (рис. 2).

Рис. 2
П4. Содержимое 2 поднятых полосок можно сравнить, чтобы определить, какая из них содержит меньшее число.
П5. Две полоски можно поменять местами в карманах. (рис. 3 по отношению к рис. 2).

Рис. 3
Я воспользуюсь тем, что вы здесь, чтобы рассчитывать на вашу помощь (предположим, что я не смог решить проблему), в группах до 3-х участников. Давайте посмотрим, какие из 3х групп решат задачу первыми; в качестве великолепного приза они получат доски, которые они использовали со своими полосками».
2.2 Практические соображения
Мы использовали белые бумажные доски размером примерно 80 см х 25 см; карманы изготовлены из цветного картона размером примерно 9 см х 9 см, скреплены скобами снизу и проклеены с левой и правой сторон. Полоски выполнены из картона другого цвета размером 5 см х 12 см, на скрытой части которых написаны цифры (до 3-х цифр). Доска может быть сложена пополам для облегчения транспортировки и хранения.
Другой вариант, менее наглядный, но гораздо более простой, — использовать 8 листов бумаги одного цвета и размера, выложенных в ряд на столе. В дальнейшем мы будем использовать описание с картонной доской и карманами.
Инструктор формулирует задачу, раздаёт лист бумаги с правилами, объясняет их с помощью доски, а затем раздаёт по одной доске каждой группе. Как правило, первым 3 группам требуется от 10 до 15 минут, чтобы найти решение проблемы.
- Полученные решения
3.1. Описание и обобщение решений
Инструктор сообщает участникам, что его менеджер собирается дать ему дополнительные задания, поэтому могут быть дополнительные доски с любым количеством карманов. Затем он обращается к участникам каждой группы-победителя за помощью, описывая метод, который они использовали, чтобы он мог его изучить. Он также просит их сделать обобщение на любое заданное число n карманов. Он просит других участников хранить молчание, обращая внимание на то, чтобы убедиться, что их решение было таким же.
Преподаватель должен помочь группам достаточно логично описать процессы, которые они выяснили. Одной из наиболее распространённых проблем является задание условия для определения того, что процесс сортировки достиг конца. После описания групп-победителей инструктор спрашивает, есть ли у какой-либо другой группы другая идея, и просит дать описание.
3.2. Типы решения
В целом участники выводят 3 самых простых и традиционных решения задачи сортировки, описанных в любом вводном тексте по алгоритмам [2]. Когда 2 выигравшие группы достигли одного и того же решения, как правило, некоторая не выигравшая группа достигла оставшегося третьего решения.
Преподаватель показывает, что 3 метода описаны в литературе, и показывает соответствующие главы в учебниках. Это очень впечатляет студентов, потому что они осознают свою способность изобретать процессы, описанные на международном уровне. Он спрашивает название, которое они дали бы своим методам, и представляет традиционные названия, используемые в литературе. Раскладіваются раздаточные материалы, показывающие каждый из методов с примерами. Для ориентации читателей, не знакомых с информатикой, мы представляем эти методы в дальнейшем; распределенные листы содержат точно такие же слова, как представлено ниже. Обратите внимание на прогрессивную эволюцию формализации алгоритма. Версия 1 показывает описание, обычно данное участниками. В следующих версиях мы постепенно приближаемся к формальному алгоритму.
3.2.1. Метод выбора
Содержимое карманов будем называть C 1 ,…,C n .
Версия 1 (неофициальное описание). Сравните C 1 с C 2 и поменяйте их полоски, если C 1 > C 2 . Затем проделайте то же самое с C 1 и C 3 , затем с C 1 и C 4 и т.д. до C 1 и C n . В конце этой фазы наименьший элемент последовательности будет в кармане 1. Теперь мы выполняем вторую фазу, сравнивая C 2 и C 3 , меняя их местами, если C 2 > C3 , затем проделав то же самое для C2 и C4, C 2 и C5, …, C 2 и C n . После этого карман 2 будет содержать второй наименьший элемент последовательности. Мы повторяем эти фазы, начиная с C 3 , затем с C 4 , до C n-1 . Затем полоски будут заказаны по желанию.
Вариант 2 (первоначальная формализация)
для i от 1 до n -1
do: сравниваем C i с C i+1 , затем с C i+2 , … , вплоть до C i с C n , меняя каждую пару полосы, если C i > C i+j .
Вариант 3 (окончательная формализация)
для i от 1 до n -1
do: для j от i +1 до n
do: если C i > C j поменять местами содержимое карманов
Пример (в таблице показана ситуация после выполнения шага, обозначенного значениями i и j ):
| i | j | карман: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| первоначальное значение: | 5 | 10 | 3 | 7 | 15 | 2 | 1 | 9 | ||
| 1 | 2 | 5 | 10 | 3 | 7 | 15 | 2 | 1 | 9 | |
| 3 | 3 | 10 | 5 | 7 | 15 | 2 | 1 | 9 | ||
| … | ||||||||||
| 6 | 2 | 10 | 5 | 7 | 15 | 3 | 1 | 9 | ||
| 7 | 1 | 10 | 5 | 7 | 15 | 3 | 2 | 9 | ||
| 8 | 1 | 10 | 5 | 7 | 15 | 3 | 2 | 9 | ||
| 2 | 3 | 1 | 5 | 10 | 7 | 15 | 3 | 2 | 9 | |
| … | ||||||||||
| 8 | 1 | 2 | 10 | 7 | 15 | 5 | 3 | 9 | ||
| 3 | 4 | 1 | 2 | 7 | 10 | 15 | 5 | 3 | 9 | |
| … | ||||||||||
| 8 | 1 | 2 | 3 | 10 | 15 | 7 | 5 | 9 | ||
| 4 | 5 | 1 | 2 | 3 | 10 | 15 | 7 | 5 | 9 | |
| … | ||||||||||
| 8 | 1 | 2 | 3 | 5 | 15 | 10 | 7 | 9 | ||
| 5 | 6 | 1 | 2 | 3 | 5 | 10 | 15 | 7 | 9 | |
| … | ||||||||||
| 8 | 1 | 2 | 3 | 5 | 7 | 15 | 10 | 9 | ||
| 6 | 7 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 9 | |
| 8 | 1 | 2 | 3 | 5 | 7 | 9 | 15 | 10 | ||
| 7 | 8 | 1 | 2 | 3 | 5 | 7 | 9 | 10 | 15 |
3.2.2. Пузырьковый метод
Версия 1 (неофициальное описание). Сравните C 1 с C 2 и поменяйте их содержимое, если C 1 > C 2 . Затем проделайте то же самое с C 2 и C 3 , затем с C 3 и C 4 , пока не появятся C n-1 и C n . В конце этой фазы наибольший элемент последовательности окажется в кармане n . Теперь мы переходим ко второй фазе, выполняя сравнения до C n-1 , получая 2-й наибольший элемент последовательности в кармане н -1. Повторяем эти фазы, проводя сравнения до C n-2 , затем C n-3 , .. и, наконец, C 2 . Затем полоски сортируются.
Вариант 2 (первоначальная формализация)
при изменении i от n до 2
do: сравнить C 1 с C 2 , C 2 с C 3 , …, до C i-1 с C i , поменяв местами каждую пару полосок их карманы, если C j > C j+1
Вариант 3 (окончательная формализация)
для i от n до
do: для j от 1 до i -1
do: если C j > C j+1 , поменять местами их полоски
| i | j | карман: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Первоначальное значение: | 5 | 10 | 3 | 7 | 15 | 2 | 1 | 9 | ||
| 8 | 1 | 5 | 10 | 3 | 7 | 15 | 2 | 1 | 9 | |
| 2 | 5 | 3 | 10 | 7 | 15 | 2 | 1 | 9 | ||
| 3 | 5 | 3 | 7 | 10 | 15 | 2 | 1 | 9 | ||
| 4 | 5 | 3 | 7 | 10 | 15 | 2 | 1 | 9 | ||
| 5 | 5 | 3 | 7 | 10 | 2 | 15 | 1 | 9 | ||
| 6 | 5 | 3 | 7 | 10 | 2 | 1 | 15 | 9 | ||
| 7 | 5 | 3 | 7 | 10 | 2 | 1 | 9 | 15 | ||
| 7 | 1 | 3 | 5 | 7 | 10 | 2 | 1 | 9 | 15 | |
| … | ||||||||||
| 6 | 3 | 5 | 7 | 2 | 1 | 9 | 10 | 15 | ||
| 6 | 1 | 3 | 5 | 7 | 2 | 1 | 9 | 10 | 15 | |
| … | ||||||||||
| 5 | 3 | 5 | 2 | 1 | 7 | 9 | 10 | 15 | ||
| 5 | 1 | 3 | 5 | 2 | 1 | 7 | 9 | 10 | 15 | |
| … | ||||||||||
| 4 | 3 | 2 | 1 | 5 | 7 | 9 | 10 | 15 | ||
| 4 | 1 | 2 | 3 | 1 | 5 | 7 | 9 | 10 | 15 | |
| … | ||||||||||
| 3 | 2 | 1 | 3 | 5 | 7 | 9 | 10 | 15 | ||
| 3 | 1 | 1 | 2 | 3 | 5 | 7 | 9 | 10 | 15 | |
| 2 | 1 | 2 | 3 | 5 | 7 | 9 | 10 | 15 | ||
| 2 | 1 | 1 | 2 | 3 | 5 | 7 | 9 | 10 | 15 |
3.2.3 Метод вставки
Версия 1 (неофициальное описание). На начальном этапе сравните C 2 с C 1 и поменяйте их полоски, если C 2 < C 1 . После этого мы можем гарантировать, что последовательность C 1 и C 2 находится в порядке возрастания. На втором этапе сравните C 3 с C 2 , поменяв местами их полоски, если C 3 < C 2 . Если был обмен, сравните C 2 с C 1 , поменяв местами их полоски, если C2 < С 1 . После этой второй фазы мы гарантируем, что последовательность от C 1 до C 3 отсортирована. Мы повторяем эти фазы, начиная с C4 , затем с C5 ,до Cn . Последняя фаза (которая начинается с Cn ) работает следующим образом: сравнивают Cn с Cn-1 и меняют местами их полоски, если Cn < C n–1; если был обмен, сравните C n-1 с C n-2 и поменять местами их полоски, если C n-1 < C n-2 ; повторять этот процесс до тех пор, пока не будет необходимости обмениваться содержимым соседней пары карманов или процесс дойдёт до сравнения и возможного обмена C 1 с C 2 .
Вариант 2 (начальная формализация)
при изменении i от 2 до n
do: последовательно сравниваем элементы пар ( C j , C j-1 ) для j от i до 2 или до тех пор, пока не найдем C j > C j-1 ;
для каждой пары из этого набора замените C j на C j-1 , если C j < C j-1
Вариант 3 (окончательная формализация)
для i от 2 до n
do: j ← i;
в то время как (C j < C j-1 ) и (j > 1 )
do: обменивают C j и C j-1 ; j ← j -1
| i | j | карман: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Первона-чальное значение: | 5 | 10 | 3 | 7 | 15 | 2 | 1 | 9 | ||
| 2 | 2 | |||||||||
| 3 | 3 | 5 | 3 | 10 | 7 | 15 | 2 | 1 | 9 | |
| 2 | 3 | 5 | 10 | 7 | 15 | 2 | 1 | 9 | ||
| 4 | 4 | 3 | 5 | 7 | 10 | 15 | 2 | 1 | 9 | |
| 3 | ||||||||||
| 5 | 5 | |||||||||
| 6 | 6 | 3 | 5 | 7 | 10 | 2 | 15 | 1 | 9 | |
| 5 | 3 | 5 | 7 | 2 | 10 | 15 | 1 | 9 | ||
| 4 | 3 | 5 | 2 | 7 | 10 | 15 | 1 | 9 | ||
| 3 | 3 | 2 | 5 | 7 | 10 | 15 | 1 | 9 | ||
| 2 | 2 | 3 | 5 | 7 | 10 | 15 | 1 | 9 | ||
| 7 | 7 | 2 | 3 | 5 | 7 | 10 | 1 | 15 | 9 | |
| 6 | 2 | 3 | 5 | 7 | 1 | 10 | 15 | 9 | ||
| 5 | 2 | 3 | 5 | 1 | 7 | 10 | 15 | 9 | ||
| 4 | 2 | 3 | 1 | 5 | 7 | 10 | 15 | 9 | ||
| 3 | 2 | 1 | 3 | 5 | 7 | 10 | 15 | 9 | ||
| 2 | 1 | 2 | 3 | 5 | 7 | 10 | 15 | 9 | ||
| 8 | 8 | 1 | 2 | 3 | 5 | 7 | 10 | 9 | 15 | |
| 7 | 1 | 2 | 3 | 5 | 7 | 9 | 10 | 15 | ||
| 6 |
3.3 Практические наблюдения
Вариант метода отбора, описанный инструктором (и уже предложенный группой), заключается в выполнении только одного обмена в каждом цикле сравнений от i до n ; для этого можно просто оставить полоску в кармане j поднятой, с меньшим числом, встречающимся от i до j , i ≤ j ≤ n ; в дальнейшем, если найдётся полоска с меньшим номером, последнюю поднимаем вверх, а первую опускаем; меньший, наконец, обменивается с i-й полосой. Несмотря на то, что мы сохранили количество сравнений, одиночный обмен уменьшает количество операций. Это начало введения идеи эффективности.
Усовершенствование пузырькового метода, на которое неоднократно указывали участники, заключается в остановке выполнения процесса сразу после фазы без обмена, потому что в этом случае последовательность уже отсортирована.
- Анализ решений
Инструктор продолжает рассказывать драму своей жизни: представив различные решения своему менеджеру, тот обязательно спросит его, какое из них лучше. Он ждёт помощи от участников, направляя их вопросами типа: «Что значит быть лучшим?»; “Как мы можем сравнить различные эффективности?”; «Какие операции требуют больше работы для выполнения?».
Преподаватель заканчивает тем, что предлагает (или подтверждает какое-то предложение одного из участников), что хорошей мерой является подсчёт в каждом случае количества сравнений и обменов мнениями.
Анализируя 3 метода, можно увидеть, что в выборочном и пузырьковом методах всегда имеется ( n -1) + ( n -2) + … + 1 = n ( n -1)/2 сравнений. В методе вставки, если последовательность изначально отсортирована, имеется n – 1 сравнений, но в худшем случае также может быть n ( n – 1)/2 сравнений. То же самое происходит с улучшенным пузырьковым методом, как описано в разделе 3.3. Что касается количества обменов, то в худшем случае метод выбора с улучшением, описанным в разделе 3.3, выполняет n -1 обменов (по одному на фазу), а остальные методы выполняют n ( n-1)/2 обмена (по одному на каждое сравнение, если полосы изначально в обратном порядке).
Инструктор сообщает участникам, что ему очень не повезло, и что его менеджер знает об этом. Поэтому его менеджер захочет узнать, какова эффективность в худшем случае. Как мы видели, в этой ситуации 3 метода выполняют одинаковое количество сравнений, но метод выбора имеет некоторое преимущество, поскольку он выполняет меньше обменов.
Исходя из этих соображений, вводится понятие сложности. В описанных случаях оно имеет порядок n 2 , пишется O ( n 2 ), что видно по подсчитанному количеству сравнений. Показано, что это означает, что при больших значениях n другими членами со степенью меньше 2 можно пренебречь. Из этого следует, что удвоение количества сортируемых элементов увеличивает в четыре раза время всей сортировки.
- Более эффективный метод
Внимание: я написал новую главу 5 гораздо более простым и наглядным методом. ВВС.
5.1. Мотивация
Инструктор рассказывает, что его менеджер, вероятно, скажет: «Вашим друзьям понадобилось 30-40 минут, чтобы найти эти решения. Если бы они работали все утро, нашли бы они более эффективное решение?». Он спрашивает участников, что они думают по этому вопросу. В общем, большинство из них думают, что можно получить лучший метод, но всегда есть те, кто считает, что лучшего метода не существует.
Затем вводится более эффективный метод, сортировка по дереву , в котором используются точно такие же правила с П1 по П5 со следующими дополнениями:
П6. Допускается использование дополнительных карманов; они следуют правилам от R1 до R5 .
П7. Можно стереть номер полоски и написать вместо неё другой.
5.2. Сортировка дерева
Метод изображается на доске следующим образом:
и) 8 цифр пишутся рядом (рис. 4).

Рис. 4
Замечено, что в предыдущих методах производилось сканирование, сравнивающее пары полосок, только для того, чтобы сохранить одну единственную часть информации: каково наименьшее (или наибольшее) число в последовательности. Другой возможностью было бы сделать только одно сканирование, но сохранить больше информации. Было бы ещё лучше, если бы мы могли при каждом сравнении оставлять результат в дополнительном кармане (точнее, копировать результат в дополнительный карман), например меньшее число.
- ii) На первом этапе сравните 8 исходных чисел, по два за раз, получив последовательность (или уровень) дополнительных карманов (рис. 5).

рис. 5
Заметьте, что если мы хотим найти наименьшее число последовательности, достаточно поискать его среди чисел на этом новом уровне.
iii) На следующем этапе мы сравниваем полученные 4 числа этого уровня два на два, в результате чего получается 3-й уровень вспомогательных карманов.
- iv) Повторяйте эти этапы до тех пор, пока не будет получен уровень только с одним карманом (рис. 6).
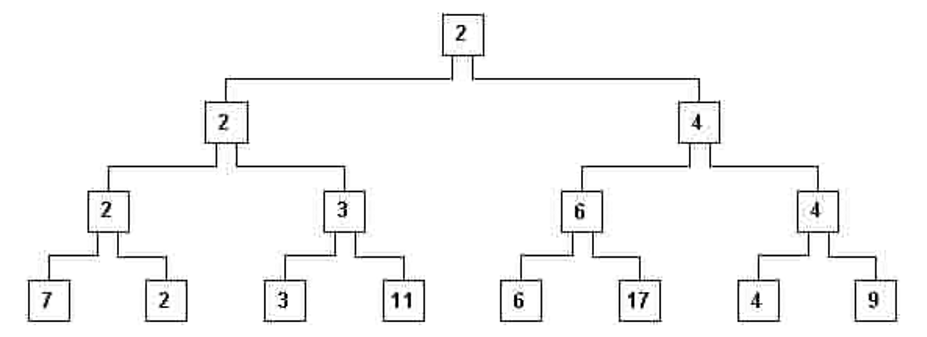
рис. 6
- v) Структура, показанная на рис.6 называетсядеревом . Каждый карман называется узлом . Самый верхний узел называется корнем , а самые нижние узлы называются листьями (дерево перевёрнуто — это обычное отношение учёных-компьютерщиков к миру после того, как они слишком интенсивно использовали свои компьютеры…). Остальные узлы называются промежуточными узлами . Узел x является родителем узла y (его дочерним элементом), если x находится на уровне непосредственно выше y и соединён с y .. Обратите внимание, что на рис. 6 каждый нелистовой узел является родителем ровно 2 дочерних узлов. Эти дочерние узлы называются родственными узлами по отношению друг к другу. Мы можем обобщить определение родительского и дочернего узлов, чтобы они были восходящими и дочерними узлами.
- vi) Обратите внимание, что наименьшее число является корнем (2 на рис. 6), потому что для каждого нелистового узла выполняется следующее свойствоП: его содержимое меньше или равно любому из его потомков. Корень содержит первый элемент упорядоченной последовательности.
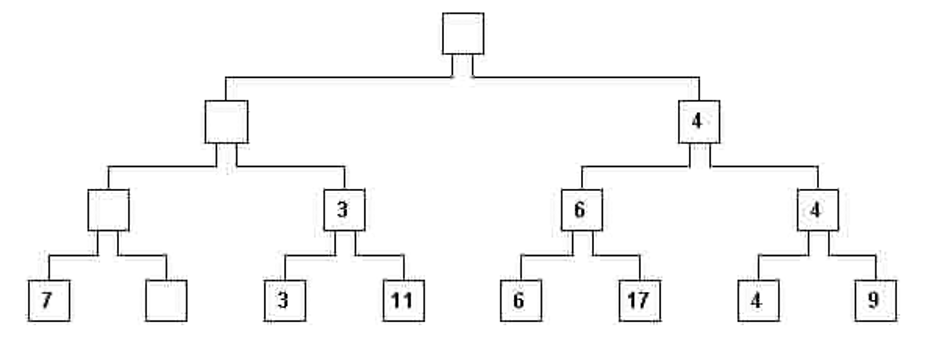
vii) Теперь мы стираем этот номер с корневого узла и со всех узлов, где он появляется (это называется иерархическим путём от корня вниз к листу), создавая пустые узлы (те, которые не имеют номера. рис. 7)
инжир. 7
Интересно отметить, что правила игры П1 – П5 продолжают действовать: достаточно поднять полоску родительского узла и одного из его дочерних узлов, чтобы решить, какой из них имеет то же значение, что и его родитель.
viii) Теперь нужно переставить дерево. Только стёртые узлы должны быть восстановлены, потому что они больше не удовлетворяют правилу П. Содержимое пустых узлов не должно использоваться в сравнениях. Начиная с пустого листового узла, мы видим, что его родственный узел (7 на рис. 7) должен быть перемещён в его родительский узел. (рис. 8).
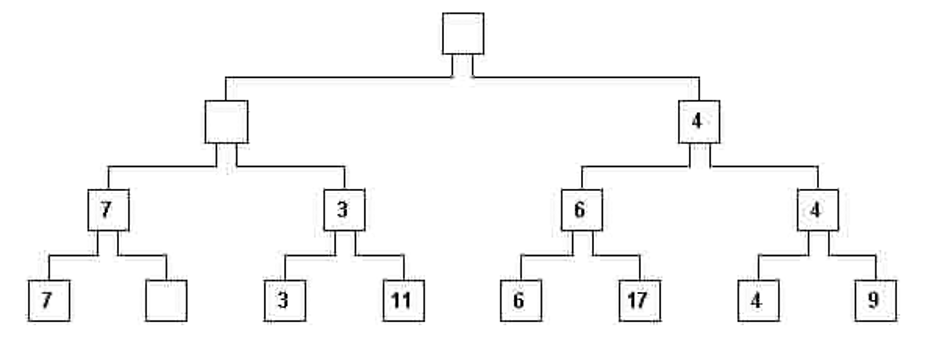
рис. 8
- ix) Было бы интересно сохранить технику сравнения, потому что иметь дело с «пустым» кажется довольно странным.Для этого мы можем спросить участников: какое число вы бы вставили в пустой лист-узел, чтобы его родственный узел (7 в примере) всегда был бы меньше?Участники всегда отвечают правильно: бесконечность! Отмечается, что в компьютерах никогда не бывает «бесконечности»; вообще мы выбираем максимально возможное число, которое можно вставить в “полосу” (слово памяти в компьютере). На доске вставляем знак бесконечности ∞ в каждую пустую вершину (рис. 9).
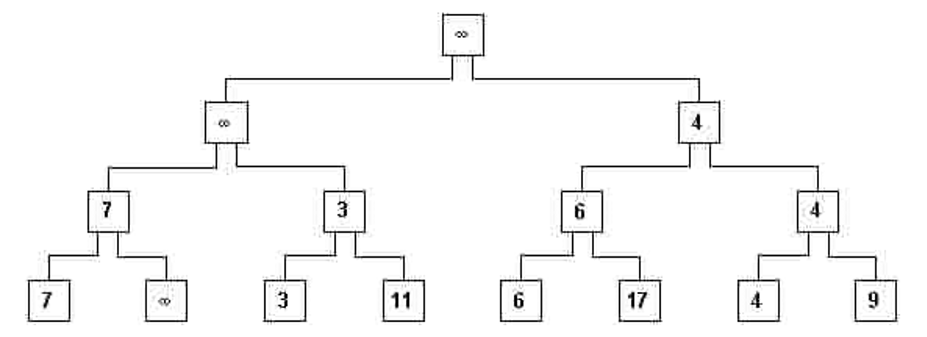
рис. 9
- x) Реконструкция дерева производится по иерархическому пути до корня, который затем будет содержать следующий элемент упорядоченной последовательности (рис. 10).
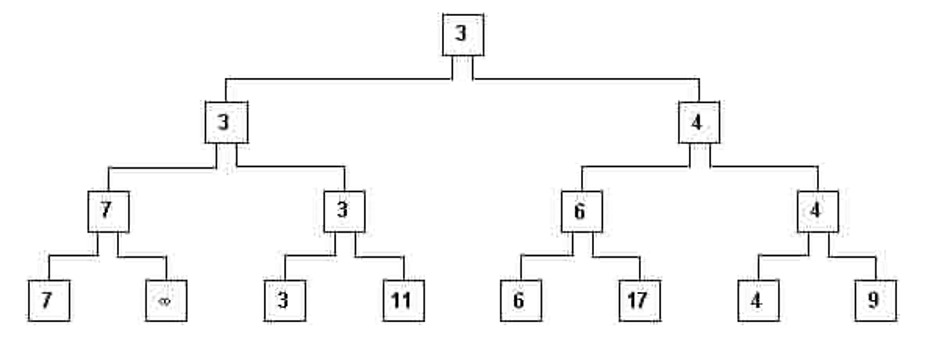
рис. 10
- xi) Новый корень устраняется, заменяя соответствующие элементы иерархического пути на ∞(рис. 11).
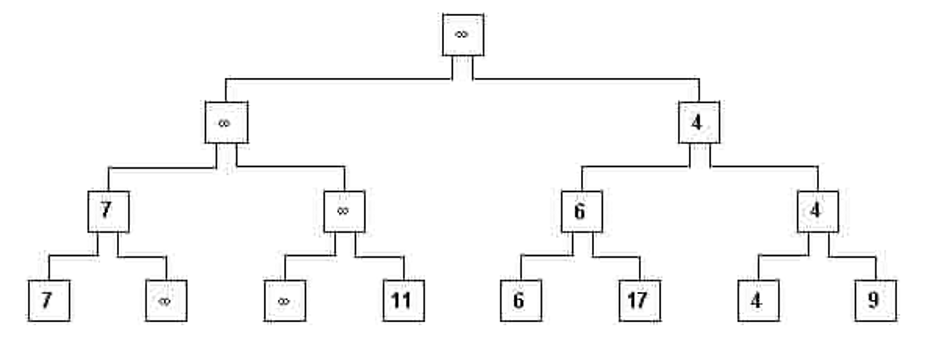
рис. 11
xii) Процесс повторяется до тех пор, пока все n чисел не будут стёрты из корня.
5.3. Анализ
Продолжим считать количество сравнений.
Для построения исходного полного дерева (рис. 6) количество сравнений равно количеству созданных вспомогательных карманов. Если листьев n , то на уровне их родителей будет n /2 карманов, затем на уровне родителей n /4 и т.д. до 1.
Как правило, в этот момент участники замечают, что n не может быть произвольным числом, предполагая, что это должно быть чётное число. Заметим, что если n не является степенью двойки, то можно дополнить листовые узлы дополнительными узлами, содержащими ∞ , до тех пор, пока число листьев не станет следующей степенью двойки. Таким образом, общее количество сравнений равно n , который является степенью числа 2,
С = 1 + 2 + 4 + … + п /4 + п /2
Имеем сумму геометрической прогрессии со скоростью q = 2; сумма C этой GP определяется как:
С = а 1 ( q k – 1) / ( q – 1) (1)
где a 1 — первый термин, а k — количество терминов (если у студентов не было геометрической прогрессии в их курсе, это был бы хороший повод вывести эту формулу, но тогда следует выделить дополнительное время или занятия.). Сколько терминов в нашем случае? Столько, сколько уровней во вспомогательных карманах.
Рассматривая рис.6, мы видим, что корневой уровень 0 имеет 1 элемент, уровень 1 имеет 2, уровень 2 имеет 2 2 , уровень 3 имеет 2 3 , …, таким образом, j (конечный уровень) имеет 2 элемента j . Но мы знаем, что 2 j = n .
Таким образом, j=log 2 n ( высота дерева). Поскольку мы ищем количество уровней от 0 до j – 1, мы имеем k = j . Таким образом , k = log 2 n . Замена в (1):
C = 1 (2 log 2 n – 1) / (2 – 1) = n – 1
Таким образом, для построения дерева необходимо выполнить n – 1 сравнений.
Замена корневого узла и каждого узла с одинаковым номером на ∞ требует log 2 n (высота дерева) сравнений на «пути вниз». После этого необходимо получить родственного узла последнего (листового) узла, в который была вставлена ∞ , и выполнять сравнения до тех пор, пока не будет достигнут корень, воссоздавая дерево. В этом «подъеме» мы имеем log 2 n дополнительных сравнений. Таким образом, для каждого значения корня имеется 2log 2 n сравнений. Так как первый корень был выведен особым образом, а последний удалять не надо, то ( n -1)2log 2 n сравнения в этих «подъёмах» и «спусках». Тогда общее количество сравнений равно:
n – 1 + 2( n -1) log 2 n
Что даёт нам сложность O ( n log 2 n ), что намного лучше, чем 3 исходных метода, которые имели O ( n 2 ). Это показано в следующей таблице с количеством сравнений в каждом случае. Участники были очень впечатлены методами порядка величины O ( n 2 ) и тем фактом, что сортировка по дереву, хотя и более сложная, имеет так много преимуществ. Обратите внимание, что 2048 элементов — это очень мало по сравнению, например, с количеством студентов в университете или количеством имён в телефонной книге.
Интересно также отметить, что «сортировку по дереву» следует использовать не во всех случаях, поскольку, как показано в таблице, до n = 16 другие методы более эффективны.
Далее подсчитывается общее количество карманов: n листьев плюс n -1 вспомогательных карманов, плюс n для сохранения элементов упорядоченной последовательности. Это дает 3 n -1, то есть этот метод использует в 3 раза больше карманов, чем исходные 3 метода. Далее упоминается, что можно использовать точно такие же вспомогательные карманы, получая так называемую «кучную сортировку» [2].
| н | п ( п -1)/2 | ( n -1)+2( n -1)log 2 n | Столбец 2 по сравнению с столбцом 3 |
| 1 | 0 | 0 | знак равно |
| 2 | 1 | 3 | на 67% лучше |
| 4 | 6 | 15 | на 60% лучше |
| 8 | 28 | 49 | на 43% лучше |
| 16 | 120 | 135 | на 12% лучше |
| 32 | 496 | 341 | в 1,4 раза хуже |
| 64 | 2016 | 819 | в 2,5 раза хуже |
| 128 | 8128 | 1905 г. | в 4,3 раза хуже |
| 256 | 32640 | 4335 | в 7,5 раз хуже |
| 512 | 130816 | 9709 | в 13,5 раз хуже |
| 1024 | 523776 | 21483 | в 24,4 раза хуже |
| 2048 | 2096128 | 47081 | в 44,5 раза хуже |
- Понятие оптимального алгоритма.
Инструктор, снова обращаясь к своему менеджеру, напоминает участникам, что последний очень требователен, и спрашивает, что его менеджер собирается спросить дальше.
В целом участники формулируют правильный вопрос: есть ли лучший метод сортировки?
Преподаватель говорит, что можно формально доказать отсутствие алгоритма сортировки, основанного на сравнении элементов последовательности, имеющей сложность меньше, чем n log 2 n. Он указывает, как можно продемонстрировать этот факт, используя дерево сравнений «сортировки по дереву»: нельзя выполнять меньше сравнений, чем показано в алгоритме. Он обращает внимание на то, что невозможно найти алгоритм сортировки (основанный на сравнениях), линейный по времени в зависимости от количества упорядочиваемых элементов. Например, если сортировка 1000 чисел занимает 1 секунду, то 2000 чисел наверняка займут более 2 секунд. Это факт, о котором не знает большинство специалистов, занимающихся обработкой данных (это утверждение основано на опыте первого автора, задавшего этот вопрос специалистам по обработке данных, которые посещали одну из сотен лекций и курсов, которые он уже прочитал).
Это понятие оптимального алгоритма весьма полезно для иллюстрации важности теории вычислений, в частности, алгоритмического анализа. Большинство профессионалов, если не все из них, удовлетворяются, когда находят алгоритм, решающий проблему, не задаваясь вопросом, существует ли лучший алгоритм и его «расстояние» от теоретического оптимума. К сожалению, компьютеры стали очень дешёвыми и быстрыми, поэтому, если алгоритм выбран и разработан плохо, а машина слишком долго выдаёт ожидаемые решения, нужно просто купить более мощный и быстрый.
Если бы менеджер инструктора запросил алгоритм линейной сортировки с использованием сравнений, знание теории позволило бы инструктору отклонить свою задачу, не потеряв при этом работу за ее невыполнение.
Проблема оптимальной сортировки решена, но есть и другие открытые проблемы, являющиеся предметом исследования в области алгоритмического анализа. Исследования проводятся как для получения лучших алгоритмов, так и для демонстрации оптимальной сложности, то есть отсутствия лучших алгоритмов, если оптимум уже достигнут.
Например, задача коммивояжёра, а именно поиск пути, по которому человек должен пройти, чтобы посетить города с минимальными затратами на поездку, все ещё остаётся открытой для поиска алгоритма с полиномиальной сложностью: каждый известный в настоящее время алгоритм имеет экспоненциальную сложность.
- Вычислительные вопросы
Используя примеры сортировки, можно познакомить с фундаментальными понятиями информатики. Например, что делает профессионал, работающий в этой области, когда сталкивается с проблемой? Он ищет алгоритмы; затем нам нужно найти то, что характеризует алгоритм. Далее он пытается формально описать найденный алгоритм и запрограммировать его. Он должен продемонстрировать правильность алгоритма и проанализировать его на предмет сложности, убедившись, что он удобен в отношении времени, затрачиваемого на обработку.
7.1. Что такое алгоритм
Алгоритм — это конечная последовательность элементарных шагов, каждый из которых содержит чётко определённую математическую операцию. Выполнение последовательности должно завершаться для любого заданного набора входных данных. Обратите внимание, что это характеристика, а не формальное определение (поскольку может быть невозможно доказать, что выполнение завершается).
7.2. Сложность получения формального описания, программирование
Задача сортировки использовала следующие шаги для решения задачи: 1) Решение конкретной задачи (сортировка 8 чисел); 2) Обобщение (сортировка произвольного числа чисел); 3) Формальное описание обобщенного метода (необходимо для последующего анализа и программирования для дальнейшего внедрения в ЭВМ).
Сложность формального описания метода решения определённой задачи стала очевидной, когда группы-победители попытались сформулировать его.
Показано, что при наличии хорошего описания его программирование для ЭВМ является тривиальной задачей. Листинги программ PASCAL, которые реализуют 3 метода сортировки, описанные в разделе 3.2. придаются (см. Приложение). Каждое утверждение кратко описано.
7.3. Корректность алгоритма
Доказательство правильности алгоритма состоит в демонстрации того, что он правильно выполняет желаемый процесс, то есть достигает желаемого решения. Существуют формальные методы доказательства правильности с использованием математической логики. В этой области есть два класса задач: доказательство правильного выполнения; и доказательство того, что выполнение завершается для любого ввода. Этот последний вопрос называется проблемой остановки .
Другой метод состоит в математическом определении проблемы, а затем преобразовании этой спецификации с использованием формальных правил (верность которых должна быть предварительно продемонстрирована) до тех пор, пока не будет получен алгоритм, который можно сформулировать на языке программирования. Эта область называется «Разработка программ посредством (формальных) преобразований». Вместо того, чтобы доказывать, что программа верна, она выводится правильным образом (одна из больших проблем с доказательством правильности программы заключается в том, что, когда она неверна, в большинстве случаев ничего нельзя сделать).
7.4. Проблемы с правильными или неправильными решениями
Рассмотрим следующую задачу: есть n городов, которые нужно соединить железнодорожными путями. Стоимость строительства каждого участка, соединяющего пару городов, известна (рис. 12). Некоторые соединения невозможны (есть озера, горы и т. д.) и не представлены. Задача состоит в том, чтобы найти единственную связанную сеть (то есть позволяющую добраться из любого города в любой другой), которую можно построить с наименьшими общими затратами на строительство.
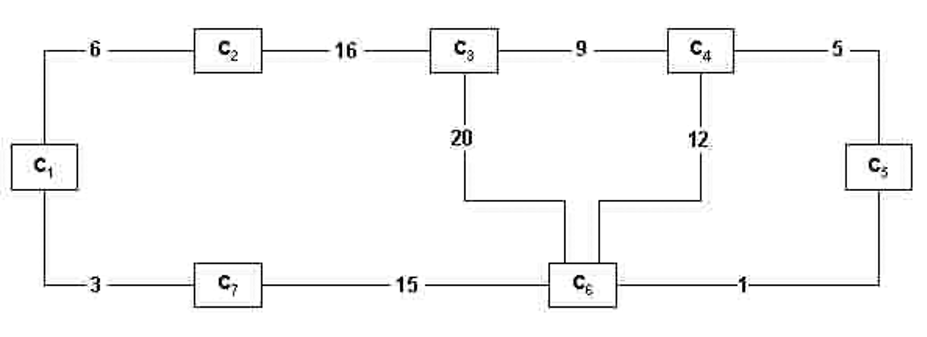
рис. 12
Крускал (см., например, [3]) предложил в 1956 году алгоритм, который классифицируется под общим названием жадных алгоритмов . Изначально разделы сортируются в порядке возрастания стоимости (заявка на алгоритмы сортировки…). Для случая рис. 12, получаем следующую последовательность (обратите внимание, что в этом примере нет двух секций с одинаковой стоимостью, поэтому стоимость идентифицирует секцию):
1 3 5 6 7 9 12 15 16 20
Далее эта упорядоченная последовательность просматривается, и на каждом шаге в заданную последовательность вставляется участок, соединяющий два города, ещё не соединённых каким-либо путём. Таким образом, шаги:
а) 1; б) 1 3; в) 1 3 5; г) 1 3 5 6; д) 1 3 5 6 9; е) 1 3 5 6 9 15
Обратите внимание, что при переходе от шага (d) к шагу (e) участок со стоимостью 7 был проигнорирован, так как он соединял два города, которые уже были косвенно связаны участком с затратами 3 и 6. Заметим также, что в ходе этого процесса можно иметь различные отключённые подсети; например, после прохода (б) у нас уже есть такая ситуация, которая остаётся таковой до последнего шага, когда соединяются две разъединённые подсети.
Полученная сеть имеет вид дерева (в примере с корнем 1 и иерархическими путями 1-5-9 и 1-15-3-6), называемого минимальным остовным деревом [3]. Крускал доказал, что он действительно имеет минимальную стоимость, тем самым решив проблему.
Интересно немного обсудить с участниками оптимальность решения: например, нельзя ли при выборе следующего участка форсировать будущий выбор более дорогих и нежелательных участков? Упоминается, что доказательство оптимальности не является тривиальным и является предметом области компьютерных наук, называемой теорией графов . Важно настаивать на важности доказательства правильности алгоритма и на том, что для нашего собственного примера он действительно выводит оптимальное решение. Это пример того, что формализация необходима для проверки некоторой интуитивной уверенности или сомнения.
Название «жадный метод» происходит от того, что на каждом шаге выбирается лучшая альтернатива. Тем не менее, это не тот метод, который приводит к оптимальному решению любой проблемы. Например, предположим, что зоолог разводит различных животных: львов, тигров, слонов, зебр, жирафов и т. д. Он получает определённую прибыль за каждое проданное им животное. Он получает заказ на определенное количество животных, независимо от вида. Проблема состоит в том, чтобы организовать только одну поездку для перевозки той смеси животных, которая даёт наибольшую общую прибыль. К сожалению, нельзя перевозить некоторых животных одновременно (его грузовик не имеет отсеков): например, львы несовместимы с зебрами — не все из последних доберутся до места назначения в целости и сохранности…
В этом случае жадный метод не даёт оптимального решения. Например, предположим, что прибыль от льва равна 20, а от зебры — 2. Есть только один лев, но 11 зебр. Жадный метод изначально выберет льва, но все зебры вместе дадут большую прибыль.
Общая проблема состоит в том, чтобы найти так называемое максимальное независимое множество . Для оптимального решения этой задачи неизвестно, существует ли алгоритм полиномиальной сложности по времени выполнения. Существующие алгоритмы используют комбинации элементов различных наборов, что приводит к факторной сложности (которая хуже, чем экспоненциальная, потому что коэффициент умножения увеличивается на 1 при каждом новом умножении). В следующем разделе мы приводим пример этой сложности, показывающий, насколько она губительна.
7.5. Проблемы с неэффективными решениями
Простой пример проблемы с неэффективным решением по своей сути следующий. Компания разработала новый ручной калькулятор с дисплеем и разрешением вычислений 8 цифр. Она хочет протестировать его, чтобы убедиться, что каждый калькулятор работает идеально. Блестящий техник решает сконструировать аппарат для проведения этих исчерпывающих испытаний.
В случае дополнений тестовый аппарат вводит 2 термина и сверяет полученный результат с ожидаемым правильным результатом. Предположим, что устройство способно проверять 1 миллион сложений в секунду (эта скорость намного выше, чем у ручных калькуляторов, потому что, если они выполняют одно вычисление каждую десятую секунды, их скорость более чем удовлетворяет их цели). Сколько времени потребуется, чтобы протестировать все возможные дополнения? В каждом термине есть 10 8 возможных различных чисел, следовательно, 10 16 возможных комбинаций значений для двух терминов. Это будет означать 10 10 секунд для выполнения всех тестов. Принимая 10000 секунд в час (вместо 3600), мы имеем 10 6часов испытаний; предполагая 25 часов в день, мы имеем 4,10 4 дня; предполагая 400 дней в году, мы имеем в общей сложности (занижено) 100 лет. То есть проблема совершенно неразрешима с помощью этого метода. (Обратите внимание, что это доказывает, что ручные калькуляторы не проходят исчерпывающую проверку… Чудо электронной техники состоит в том, что с помощью всего лишь нескольких тестов можно сделать вывод о «правильности» всей машины.)
В общем, задачи игрового моделирования носят такой характер: необходимо проверить множество комбинаций (возможных ходов в каждой ситуации). Это делает их иногда невозможными для лечения с помощью компьютеров, если только не применяются стратегии устранения многих комбинаций. Это предмет, охватываемый областью алгоритмов (ошибочно) называемой «Искусственный интеллект». Интересно отметить, что эти алгоритмы имеют очень мало общего с тем, как мы играем в соответствующие игры. На самом деле гроссмейстер в шахматах не может знать и описать процесс интуиции, который заставляет его угадывать лучший ход для каждой ситуации.
- Результаты
С помощью описанных мероприятий осуществляется введение в широкую область фундаментальных понятий теории вычислений. Как было показано, это введение начинается с физического манипулирования участниками, что позволяет избежать чрезмерно абстрактного метода обучения, не имеющего связи с реальностью учащихся. Экран компьютера не может заменить физическую активность учащихся, поскольку последние могут иметь дело с реальными, а не абстрактными объектами. Кроме того, наше предложение включает в себя социальный аспект через формирование групп, которые могут не только дискутировать в сфере идей, но и могут «делать своими руками». Чисто абстрактный уровень достигается позже, но связан с физическим опытом. В этом смысле мы имеем здесь пример обучения «снизу вверх», который кажется нам гораздо более адекватным. Конкретный пример предшествует абстракции; когда последнее будет достигнуто, учащиеся не будут считать его чем-то совершенно странным, находящимся вне их опыта.
Наш опыт показал, что физическая активность стимулирует творческие способности. Фактически, участники заявляли, что они никогда не нашли бы алгоритмы, которые они нашли, если бы они не манипулировали полосками карт. В ходе практической деятельности студенты сталкиваются с некоторыми ранее изученными математическими понятиями: суммированием числовых прогрессий, логарифмами и их свойствами, комбинаторикой. В двух оценках, написанных участниками сразу после занятия, были обнаружены следующие фразы:
«Эта деятельность актуальна в основном для тех, кто понятия не имеет, зачем они изучают математику в школе. На приведённых конкретных примерах можно понять, почему так много теории».
«Я мог бы лучше понять тот факт, что мы действительно собираемся использовать математику, изучаемую в школе».
Педагогический материал и правила игры (см. раздел 2) были разработаны таким образом, чтобы решения, найденные участниками, могли быть выражены через алгоритмы и были близки к компьютерной программе. Мы считаем важным изменить представление студентов о компьютерах и вычислительной технике. Представление, которое они имеют в настоящее время, является ложным из-за использования электронных игр, сложных текстовых и графических редакторов и т. д. и связанных с ними эмоций. Студенты нашего вводного курса информатики неизменно разочаровывались в его концептуальной форме: у них были другие ожидания. Таким образом, тот факт, что в описанных здесь действиях не используется компьютер, ведёт к изменению этой ложной идеи. Один из участников написал: «Урок показал мне, что пройти курс компьютерных наук не значит проводить за компьютером весь день».
На момент написания этой статьи, в 1993 году, было проведено 11 занятий, в которых обучалось около 450 учеников. Подавляющее большинство из них написали в своей оценке, что у них не возникло затруднений при следовании представленным алгоритмам и их анализу.
Существует много преувеличений по поводу использования компьютеров в школах. Первый автор высказал мнение, что компьютеры следует использовать только в старших классах средней школы при обучении практическому использованию компьютеров [6, 7]. В рамках другой организованной им образовательной программы «День компьютера» продолжительностью 8 часов [5] было показано, что в целом учащиеся до 17 лет не проявляют интереса к концептуальным и структурным аспектам компьютерной программы. компьютер: они хотят только поиграть с ним. Поэтому он рекомендует применять упражнения, описанные в этой статье, к этому возрасту, то есть к старшеклассникам. Им может предшествовать знакомство с внутренней логической структурой компьютеров посредством действий, также разработанных первым автором: театральная постановка, имитирующая внутреннее функционирование компьютера [8], а также изучение и использование машинного языка очень простого смоделированного компьютера [4]. У нас была возможность показать здесь, как новые, важные и широкие понятия могут быть введены таким образом, чтобы некоторые фундаментальные аспекты вычислительной техники стали понятны студентам. Наконец, мы считаем, что математика является подходящим предметом для деятельности, описанной здесь. Вычисление, с алгоритмической точки зрения, является математической наукой.
использованная литература
[1] Сетцер, Фольксваген и Р. Хирата-младший. Алгоритм и его анализ: вводное исследование . Сан-Паулу: Caderno da Revista do Professor de Maemática , Бразильское математическое общество, Vol. 4, № 1, 1993. С. 1-38.
[2] Вирт, Н. Алгоритмы и структуры данных . Энглвудские скалы: Прентис-Холл, 1986.
[3] Харел, Д. Алгоритмика – дух вычислений . Чтение: Аддисон-Уэсли, 1987.
[4] Setzer, VW & R.Hirata Jr. HIPO-PC: обучающее программное обеспечение для ознакомления с компьютерами (на португальском языке). Технический отчет RT-MAC-8809 . Сан-Паулу: кафедра компьютерных наук Университета Сан-Паулу (USP), 1989 г. Исполняемые версии симулятора HIPO-PC на английском и португальском языках доступны по электронной почте через первый редактор.
[5] Сетцер, В. В. и Р. Хирата-младший. День компьютера: краткое введение в компьютеры и вычислительную технику (на португальском языке). Ciência e Cultura 42, 5/6 (май/июнь 1990 г.), стр. 333–340, перепечатано в том же издании, что и [1].
[6] Сетцер, VW Компьютеры в образовании . Эдинбург: Floris Books, 1989. См. также расширенное издание на немецком языке Computer in der Schule? Эти и аргументы . Штутгарт: Verlag Freies Geistesleben, 1992.
[7] Сетцер, Фольксваген и Л.В.Монке. Альтернативный взгляд на компьютеры в образовании: почему, когда, как. Будет опубликовано в 2000 году издательством Humpton Press в качестве главы книги под редакцией Р. Муффолето, также доступной на веб-сайте первого автора.
[8] Сетцер, В. В., «Бумажный компьютер» — педагогическая деятельность по ознакомлению с основными понятиями компьютеров», доступно на веб-сайте первого автора (см. адрес выше).
ПРИЛОЖЕНИЕ
Программы на ПАСКАЛЬ
Program Selection;
{ Учитывая N и последовательность из N чисел, сортирует их в порядке возрастания }
{ по методу выбора. В конце печатает упорядоченную последовательность. }
Var
N, { Количество элементов в последовательности }
I, J: integer; { Индексы }
C: array[1..100] of real; { Последовательность содержит не более 100 элементов }
Aux: real; { Вспомогательная переменная, используемая при обмене }
{ содержимого 2-х карманов. }
Begin
{ Введите последовательность }
write(’Введите размер последовательности, меньше или равный 100’);
readln(N);
for I:=1 to N
do begin
write(’’Введите следующее число последовательности’’);
readln(C[I])
end;
{ Cортировать }
for I:=1 to N-1
do for J:=I+1 to N
do if C[I] > C[J]
then begin { Обменять C[I] на C[J] }
Aux:=C[I];
C[I]:=C[J];
C[J]:=Aux
end;
{ Распечатать }
writeln(’Упорядоченная последовательность:’);
for I:=1 to N
do write(C[I],’ ’);
end.
Program Пузырь;
{ Дано N и последовательность из N чисел, сортирует их в порядке возрастания }
{ методом пузырька. В конце печатает упорядоченную последовательность.. }
Var
…
Begin
…
{ Сортировать }
for I:=N downto 2
do for J:=1 to I-1
do if C[J] > C[J+1]
then begin { Обменять C[J] на C[J+1] }
Aux:=C[J];
C[J]:=C[J+1];
C[J+1]:=Aux;
end;
…
end.
Program Insertion;
{ Учитывая N и последовательность из N чисел, сортирует их в порядке возрастания }
{ по методу вставки. В конце печатает упорядоченную последовательность. }
Var
…
Begin
…
{ Сортировать }
for I:=2 to N
do begin
J:=I;
while (C[J] < C[J-1]) and (J > 1)
do begin { Обменять C[J] на C[J-1] }
Aux:=C[J];
C[J]:=C[J-1];
C[J-1]:=Aux;
end;
end;
…
end.