Оригінальна стаття
Розфарбовування графа МакГрегора
У квітневому випуску журналу Scientific American за 1975 рік Мартін Гарднер у своїй колонці «Математичні ігри» опублікував перелік шести основних математичних відкриттів 1974 року народження, про які «з тієї чи іншої причини недостатньо повідомлялося як науковому спів-товариству, так і громадськості в цілому». Одним з них бaув планарний граф зі 110 вузлами, що приписується Вільяму МакГрегору з Ваппінгерс-Фоллс, штат Нью-Йорк, який, за його твердженнями, не можна розфарбувати менш ніж в 5 кольорів, тим самим спростовуючи поки ще не доведене припущення про те, що 4х кольорів досить для фарбування будь-якого планарного графа. Це не сподобалося багатьом читачам, ще місяць опісля публікації номеру. Детальніше про історію можна прочитати тут.
Ось графік, намальований у вигляді карти
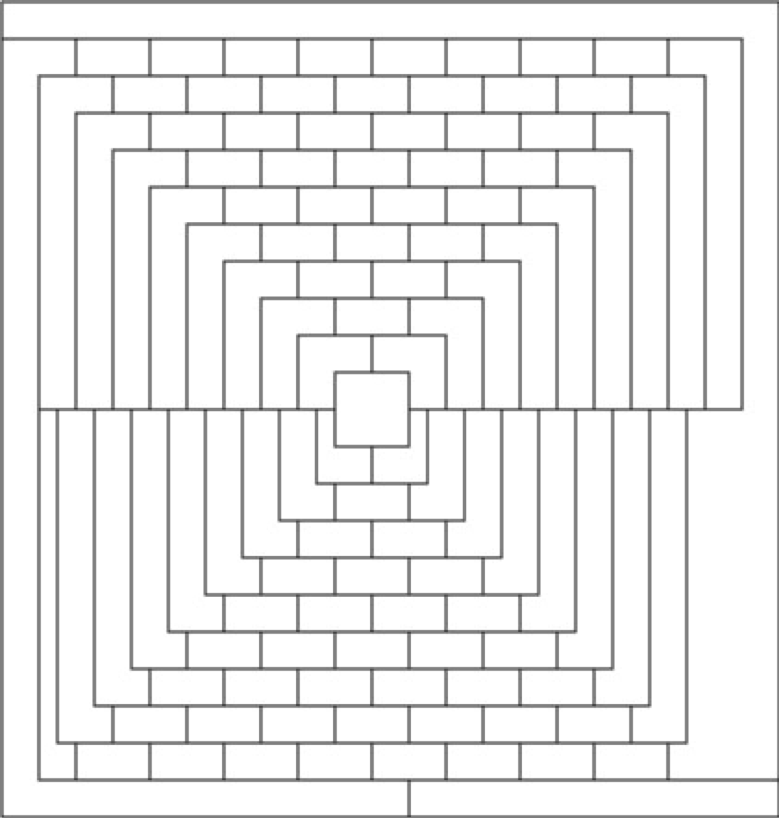
Спроба закодувати можливе забарвлення цього графа як BDD практично нездійсненна. Я припускаю, що для цього буде потрібно більше одного мільярда вузлів (оскільки мінімальний розріз графа має ширину 20 вузлів, і BDD потрібно експоненціально кодувати майже всі комбінації кольорів для цих вузлів).
Розфарбування графіка як завдання SAT
З іншого боку, розфарбування графа за допомогою вирішувателя логічної здійсненності (SAT) цілком можлива. Вирішувачу потрібно знайти тільки одне можливе рішення, тому перед ним не стоїть складне завдання кодування всіх можливих розмальовок. Ось кольори, створені вирішувачем ZChaff, який пропрацював менше ніж одну секунду на портативному комп’ютері.

Подивіться наступне відео на Youtube, що показує, як просувається цей пошук: https://youtu.be/0gt503wK7AI
Також можна змусити вирішувач генерувати «збалансовану» розмальовку, зажадавши від нього знайти рішення, використовуючи два кольори (зелений і синій) 27 раз і два кольори (червоний і жовтий) 28 разів.

Вирішувачі SAT також можуть використовуватися для вирішення завдань оптимізації, виконуючи серію викликів вирішувачів для виконання довічного пошуку по цільовій функції. Якщо ми попросимо вирішувальну програму знайти розмальовку, яка спочатку мінімізує кількість вузлів, забарвлених в зелений колір, а потім мінімізує число, забарвлене в синій колір, а потім в червоний, ми отримаємо розмальовку всього з 7 зелених вузлів, 34 синіх і червоних і 35 жовтих.

На підставі подальших експериментів можна констатувати, що до призначення кольорів це рішення має унікальні властивості:
- Це єдине забарвлення, в якому один колір використовується не більше 7 разів.
- Це єдине забарвлення, в якому один колір використовується не менше 35 разів.
Останнє поновлення: середа, 12 травня, 10:19:05 EDT 2010