СУПЕР-ВРЕМЕННОЕ-ПОШАГОВОЕ УСКОРЕНИЕ ЯВНЫХ СХЕМ ДЛЯ ПАРАБОЛИЧЕСКИХ ЗАДАЧ
COMMUNICATIONS IN NUMERICAL METHODS IN ENGINEERING, VОL. 12, 31-42 (1996)
ВАСИЛИОС АЛЕКСИАДИС
Математический факультет университета в Теннесси, Ноксвилл, штат Теннесси, США 37996-1300 и математических наук
Секция, Национальная лаборатория Ок-Ридж, Ок-Ридж, TN 37831-6367, США
GENEVGVE AMIEZ
Laboratoire de Calcul Scientifrque, Universitt de Franche-Comit, 25030 Безансон, Франция
А ТАКЖЕ
ПЬЕР-АЛЕН ГРЕМО
Департамент математики и Центр исследований в области научных вычислений, Государственный университет Северной Каролины,
Роли, Северная Каролина 27695, США
РЕЗЮМЕ
Цель статьи – привлечь внимание компьютерного сообщества к давно упускаемому из виду, очень
простому методу ускорения, который впечатляюще ускоряет явные схемы временного шага (этапов), практически без привлечения дополнительной стоимости. Авторы объясняют основу метода – стабилизацией с помощью грамотно выбранных этапов, что бы обосновать его для линейных задач и объяснить , насколько просто его включить в любой явный код для параболических задач. Наконец, мы демонстрируем его производительность на (линейном) уравнении теплопроводности, а также на (нелинейной) классической проблеме Стефана, сравнивая её со стандартными неявными схемами (использующими
итерации SOR или Ньютона). Результаты показывают, что супер-пошаговый режим более эффективен, чем неявные схемы в том, что он работает, по крайней мере, так же быстро, имеет сопоставимую или лучшую точность и, конечно, проще программировать (и распараллеливать для распределенных вычислений).
КЛЮЧЕВЫЕ СЛОВА
явная схема; неявный пошаговый режим схемы; ускорение; Чебышевский параболический; уравнение теплопроводности; Проблема Стефана
- ВВЕДЕНИЕ
Супер-пошаговый режим – очень простой и эффективный способ ускорить явный пошаговый режим алгоритма для параболических задач. Метод не новый. Концептуально он принадлежит к классу известных в сообществе численного анализа ODE как методы Рунге-Кутта-Чебышева (см. [1,2] и ссылки в них). Такие методы имеют долгую историю и постоянно используются и открываются заново. Вариации этих методов также существуют в числовой линейной алгебре (полуитерационный метод Чебышева; см., например [3]), что неудивительно, поскольку многие итерационные алгоритмы решения линейных систем допускают некоторую временную интерпретацию.
Однако, несмотря на то, что методу почти 20 лет, [4] кажется, что вряд ли любой знает об этом в вычислительном мире PDE . Это прискорбно, поскольку этот метод не только очень прост в использовании, но и впечатляюще эффективен. Фактически, супер-пошаговый режим (STS) освобождает явную схему от ограничения стабильности на временном шаге, делая её столь же удобной, как любая неявная схема, сохраняя при этом простоту и лучшую точность. Наши вычислительные результаты подтверждают это, показывая, что супер- пошаговый режим более эффективен, чем стандартные неявные схемы (с использованием итераций SOR или Ньютона), в том смысле, что они работают, по крайней мере, так же быстро, имеют сопоставимую или лучшую точность, и , конечно, их намного проще программировать (и распараллеливать для распределенных вычислений).
Наша цель в этой статье , является двоякой. Во-первых, это прямое развитие (как вариант) метода и его обоснование для линейных уравнений. Алгоритм супер-временного шага:
Основанный на ослаблении требования (сильной) устойчивости в конце каждого временного шага, чтобы требовать этого только в конце цикла, состоящего из N из них [1, 6] Представленная здесь схема является вариантом метода Генча [6]. Во-вторых, это демонстрация эффективности метода и сравнение его с неявными схемами. Мы представляем подробные сравнения производительности на (линейном)
уравнении теплопроводности на (нелинейной) задаче Стефана. Главный интерес здесь заключается в том, что STS очень хорошо работает не только в линейном случае, но и в нелинейных задачах, даже хотя, в последнем случае, не теоретические результаты не доступны. Хорошее поведение STS-подобных алгоритмов для такого рода вырожденных нелинейных параболических задач также наблюдались в ссылка [7].
План статьи выглядит следующим образом. В разделе 2 мы выводим и анализируем сверхвременнную ступенчатую схему в случае линейного параболического уравнения. Вопросы, связанные с реализацией: рассматривается в разделе 3. Раздел 4 посвящен оценке производительности как линейного, так и
нелинейных случаев. Выводы представлены в разделе 5.
- СУПЕР-ВРЕМЕННАЯ ПОШАГОВАЯ СХЕМА
Пусть мы рассмотрим этот раз , в зависимости от задачи:
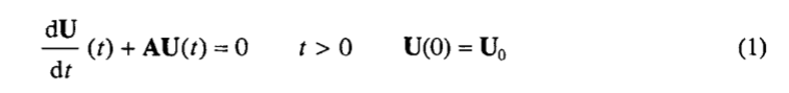
вместе с соответствующей стандартной явной схемой,
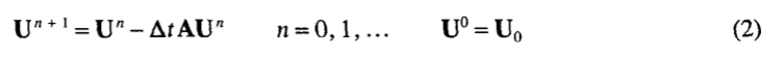
где A – симметричная положительно определенная матрица M x M , Δt > 0 – временной шаг, а U0 – заданный вектор RM. Как хорошо известно, алгоритм, что приведён выше, является предметом ограничительного стабилизационного условия

где p (.) обозначает спектральный радиус. Если λmax обозначает наибольшее собственное значение матрицы A, то последнее условие является эквивалентным.

Это знаменитое условие устойчивости Куранта-Фридрихса-Леви (CFL). Например, в
случае одномерного уравнения теплопроводности ut= αuxx , дискретизированного стандартными второго порядка различиями по равномерной сетке, мы имеем 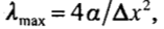 и поэтому
и поэтому 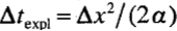 .
.
Чтобы ослабить ограничительный характер последнего условия, нам не нужна стабильность на конец каждого временного шага Δt, а скорее в конце цикла из N временных шагов, что приводит к методу Рунге-Кутта c N стадиями. Введем супершаг ΔT, состоящий из N временных шагов τ1 , τ 2 , . . . , τ N . Теперь идея состоит в том, чтобы обеспечить стабильность на супер шаге при попытке чтобы максимизировать его продолжительность 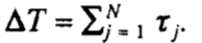 .
.
Следует подчеркнуть в этот момент , что только значения в конце каждого супер шагового ΔT приближает решение проблемы. Внутренние значения не имеют аппроксимирующих свойств
и должны рассматриваться только как промежуточные вычисления.
Новый алгоритм можно записать как
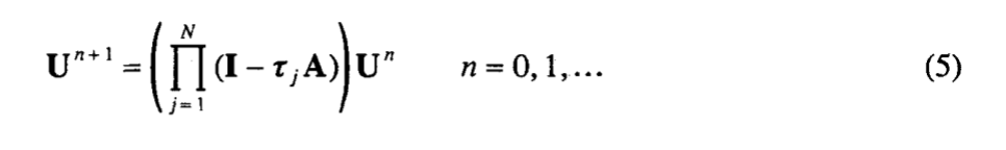
Соответствующее условие устойчивости при этом

Это соотношение выполняется, если
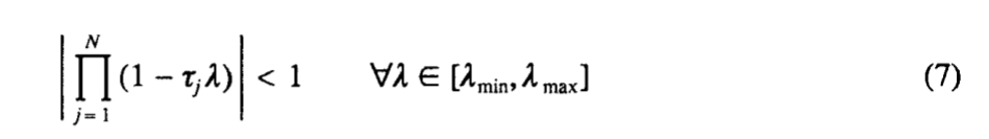
где 0 <λmin обозначает наименьшее собственное значение A. Среди бесконечного множества вариантов для τjs удовлетворяющий (7) , ищем оптимальную, а именно такую, которая делает
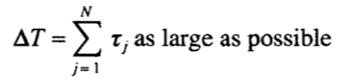 как можно больше
как можно больше
Однако вышеупомянутая проблема не так хорошо поставлена, как указано, потому что в (7) мы имеем <, а не ≤.
Для получения «сильной» устойчивости заменим условие (7) на
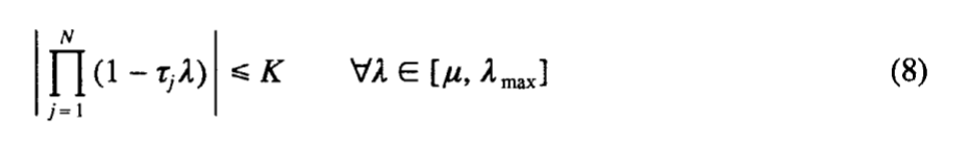
где μ – некоторое число из интервала 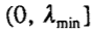 , а K – некоторое число 0 < K < 1 . Задача поиска “оптимальных” значений tjs можно переформулировать как
, а K – некоторое число 0 < K < 1 . Задача поиска “оптимальных” значений tjs можно переформулировать как
Найти t1 ,, t2, …, tN такое, что 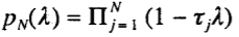 удовлетворяет
удовлетворяет
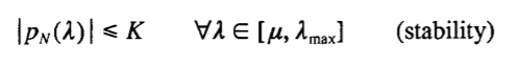 (стабильность)
(стабильность)
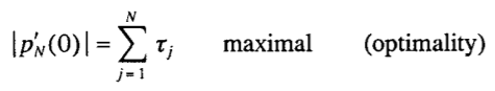 максимальный
максимальный
(оптимальность)
Используя замечательные свойства оптимальности многочленов Чебышева TN (.) Степени N,
Маркова [8](1892!), То если K определяется выражением
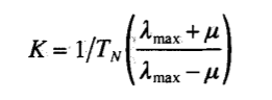
то оптимальные значения zjs – это те, для которых
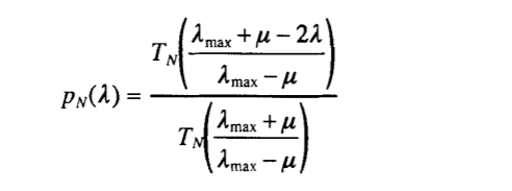
Обратите внимание, что при желании, K можно выбрать произвольно близким к 1, выбрав μ достаточно малым.
Более того, z j s, соответствующие указанному выше многочлену pN , явно задаются формулой
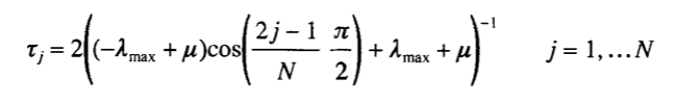
что удобнее записать как
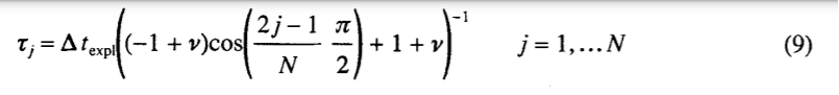
где 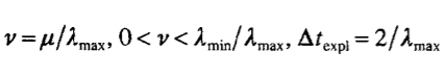 как в (4). Можно показать соотношение
как в (4). Можно показать соотношение
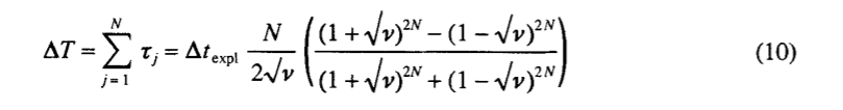
которе дает

Отметив, что N явных шагов, каждый длиной Δtexpl, покрывают время ΔNtexpl, мы видим, что выполнение супершага, состоящего из N подшагов, покрывает временной интервал в N раз больше (при v 0). Таким образом, супершаговый шаг в (до) N раз быстрее, чем стандартная явная схема, по существу при той же стоимости! Это проявляется , там где увеличивается скорость.
Заметим, что ошибка между точным и приближенным решениями определяется выражением
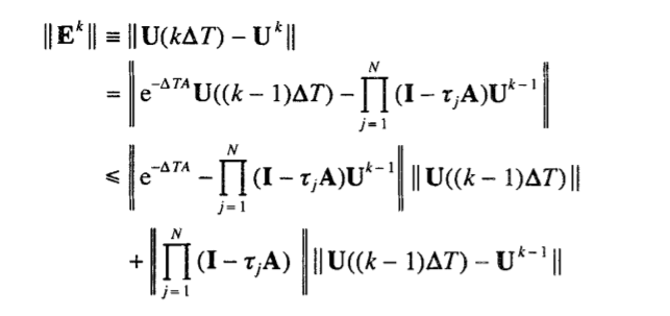
Поскольку A положительно определена, имеем
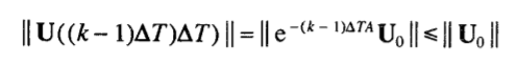
С другой стороны, мы замечаем, что симметричность A означает, что 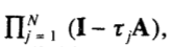 . И таким образом условие стабильности (6) эквивалентно
. И таким образом условие стабильности (6) эквивалентно 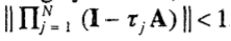 Собирая все это вместе, получаем
Собирая все это вместе, получаем
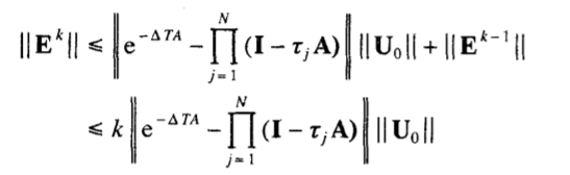
Расширяя и сохраняя только члены низшего порядка, получаем
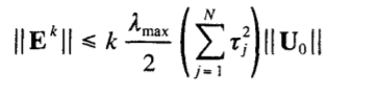
Как и ожидалось, метод является по существу первого порядка по отношению к ΔT. Если v увеличивается, то длина каждого из τjs уменьшается , и, с учетом последнего соотношения, является как ошибка, при этом за счет большего количества вычислений. Длина супершага (определяется спектральными свойствами A, и выбором N и v) ограничена только точностью, как и с любой безусловно устойчивой неявной схемой.
Заметим, что случай μ = v = 0 соответствует пределу устойчивости. Поэтому выбор v слишком маленькиим может привести к методу, очень чувствительному к ошибкам округления. Ситуацию можно исправить, если слегка увеличивать v, или использовать подходящую перестановку внутренних шагов (см., например, [ 6]).
Стоит отметить, что, хотя мы оправдываем метод только в том случае, если оператор A появляется в (1) является симметричной положительно определенной матрицей, такое предположение не всегда оказывается верным что требуется на практике. Важным практическим случаем является случай итерационной матрицы A, допускающей комплексные собственные значения, как это может иметь место в задачах конвекции-диффузии. Мы показываем в следующий пример, что цена, которую нужно заплатить за ускорение метода, составляет лишь небольшую уплощение области устойчивости в комплексной плоскости.
Действительно, мы рассмотрим случай супер шага с двумя внутренними шагами против двух шагов стандартной явной схемы. Обозначим через G оператор дискретной итерации, фигурирующий в (5), в терминах из которых область устойчивости на комплексной плоскости равна 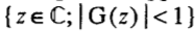 . Грубо говоря, переменная z теперь играет роль Δtexpl, A. Используя (9), имеем
. Грубо говоря, переменная z теперь играет роль Δtexpl, A. Используя (9), имеем 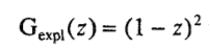 , для двух шагов явной схемы
, для двух шагов явной схемы 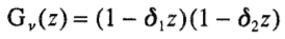 для метода STS с двумя внутренними шагами где
для метода STS с двумя внутренними шагами где 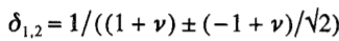 . В этой нормализованной структуре длина супер щага это больше , чем два стандартных шага если
. В этой нормализованной структуре длина супер щага это больше , чем два стандартных шага если 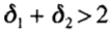 . На рисунке 1 (а) показана область стабильности для Gexpl, (кружок) и Gv, для v = 0; 0,04; 0,08; 0,12; 0,16; 0,20; для которых
. На рисунке 1 (а) показана область стабильности для Gexpl, (кружок) и Gv, для v = 0; 0,04; 0,08; 0,12; 0,16; 0,20; для которых 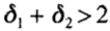 соответственно равно 4; 3,35; 2,90; 2,58; 2,34; 2,14.
соответственно равно 4; 3,35; 2,90; 2,58; 2,34; 2,14.
Области устойчивости увеличиваются с увеличением v. Опять же, v = 0 соответствует пределу устойчивости, имеет наименьшую область устойчивости (∞ -образное основание), и это явно не для рассмотрения для любой практической цели. На рис. 1 (б) показаны области устойчивости для N = 3.
Другими словами, ускорение, вплоть до фактора Н, обеспечивается супер шаговым алгоритмом, получают при очень малой цены небольшого уменьшения области устойчивости по мнимой оси (что сопровождается увеличением по действительной оси).
Наконец, как будет ясно из многочисленных экспериментов, представленных в следующих разделах, СТС работает очень хорошо не только в линейном случае, который мы здесь обосновали, но даже
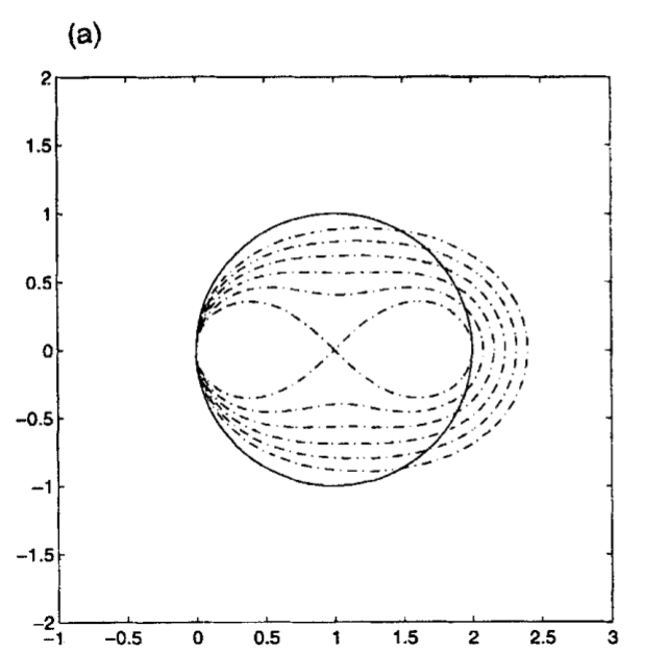 Рис. 1 (а)
Рис. 1 (а)
Рис. 1 (б)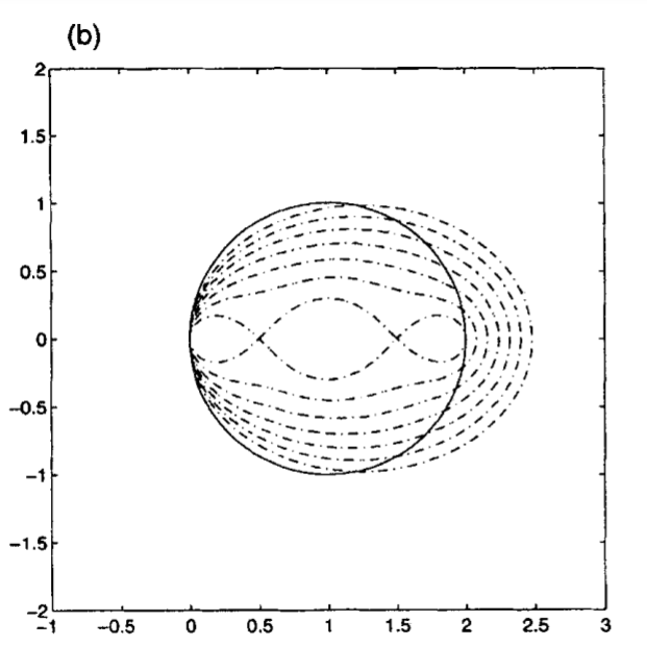
На рис. 1.а область устойчивости стандартной явной схемы (кружок) и STS с различными значениями v для N = 2 (Рисунок 1а), а для N = 3 (Рисунок 1.b).
когда A представляет собой нелинейный оператор. Теоретические трудности в обосновании нелинейного случая возникает из-за того, что для зависящего от времени семейства матриц A (t) симметрия продукта 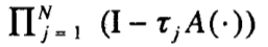 больше не гарантируется коммутативностью терминов входа в эти продукты.
больше не гарантируется коммутативностью терминов входа в эти продукты.
- РЕАЛИЗАЦИЯ
Супер-временной пошаговый алгоритм может быть легко применён к любому явного времени пошагового алгоритма в виде (2), как, в частности , для параболических задач.
Несмотря на то, что спектральные свойства оператора A играют важную роль в теоретическом обосновании, представленное в разделе 2, точное знание этих свойств невозможно, хотя и требуется для реализации. Метод является надёжным в этом отношении. Это правда не только примеры, представленные ниже, но и в целом, как, к примеру, в трех-мерные промышленных вычислениях в [ 7]. Там определяют явный временной шаг Δtexpl, обычным способом для удовлетворения условия CFL, но вместо выполнения шагов длины Δtexpl выполняет супершаги длины ΔT следующим образом: выбираем N, v и выполняем N подшаги τ1 , τ2, …, τN из (9), без вывода до конца каждого супершага. Единственные дополнительные расходы , это тривиальное вычисление в (9), в то время как выполнение будет ускорено до коэффициента N.
Если нужно интегрировать (1) до момента времени T, стандартный явный метод требует не менее nexpl, = T / Δtexpl один явный шаг, где все вычисленные значения являются приближениями к решению.
Небольшой шаг по времени, навязанный схеме стабильностью, даёт высокую точность, которая часто превосходит требования пользователя и достигается за счёт высокой стоимости. С другой стороны, и СТС, и неявные методы позволяют выбирать (супер) шаг по времени ΔT сколь угодно большим. Выбор здесь основан на точности , а не требования стабильности STS с N внутренними шагами выполняется на наименьшее количество явных шагов NT / ΔT , где ΔT определяется как (1o), и дает приблизительное значение T / AT значения решения. Неявный метод , дающий одинаковое число приближенных значений требует только неявных шагов T / ΔT , но каждый из них вычисляется неопределённым числом итераций. Таким образом, супер-пошаговый режим эффективно освобождает явную схему от устойчивости ограничения на шаг по времени, что делает её такой же удобной, как и любую неявную схему, при этом сохраняется её простота и лучшую точность.
Заметим, что наш подход, как и в [ 4, 6, 7], отличается от подхода, пропагандируемого в [ 1, 2, 5]. Мы рассматриваем факторизованную реализацию в последовательности явных шагов, в отличие от использования трёхчленной рекурсии и так называемого диагонального выполнения. Последнее может обеспечить лучшую внутреннюю стабильность, то есть устойчивость внутренних ступенек.
Однако, как показано в следующих примерах и как замечено в [ 4, 7], внутренние проблемы со стабильностью, похоже, не искажают решение сверх очень приемлемых уровней. В факторизованной реализации имеется большое преимущество в том, что она может быть включена непосредственно в существующий явный код, как описано выше. Кроме того, поскольку это одношаговый метод, он требует меньше памяти, чем в диагональной реализации, в которой используется два шага. Наконец, поскольку наша реализация не полагается на точное знание спектральных свойств, она может быть применена к сложным задачам, а не только к нескольким задачам из учебников.
- ВЫПОЛНЕНИЕ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ ЗАДАЧ.
Мы исследуем производительность схемы супер-шага по времени на двух точно решаемых моделях.
Задачи: простая задача теплопроводности (линейная) и классическая двухфазная задача Стефана (нелинейная), в одном пространстве. В каждом случае мы сравниваем со стандартными версиями схема Кранка-Николсона и / или полная неявная схема, одна с использованием SOR, а другая – итераций Ньютона для решения полученной системы. Имеются следующие проблемы модели.
4.1. Проблема I
Рассмотрим нагрев плиты при x >0, первоначально при (нормированной) температуре u (x, 0) = 0, когда u = 1 при x = 0. Предполагаемые постоянные теплофизические свойства, в безразмерных переменных температуры u (x, t) удовлетворяет уравнению теплопроводности ut, = uxx . Задача допускает точное (подобие) решения в терминах функции ошибок, задаваемой формулой
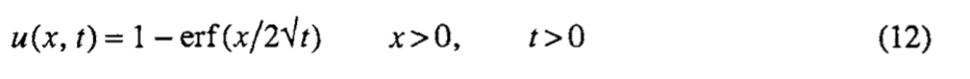
4.2. Проблема 2
Рассмотрим плавление сляба при x>O, первоначально твердого при (нормированной) температуре u (x, 0) = – 1 из-за того, что u = +1 наложено при x = 0. Фронт расплава x = X (t) возникает из x = 0 при t = 0, отделяя жидкость в O⩽x<X (t) от твердого тела в X (t) <x, t> O. Предполагая постоянные теплофизические свойства и, для простоты, одинаковые в обеих фазах, в безразмерных переменные неизвестная температура u (x, t) и граница раздела X (t) удовлетворяют9 уравнению теплопроводности ut = uxx, в обеих фазах, и интерфейсные условия u(X(t), t) = 0 и X‘(t) = St [-u, (X (t)–, t) +uх(X (t) +, t)], где St обозначает число процесса Стефана (отношение ощутимое к скрытому теплу, здесь равняется единице по скрытому теплу из-за нашей нормализации). Это является одной из немногих точно решаемой задачи фазового перехода, допускающие решение по подобию (известное как Решение Неймана) через функцию ошибок )[9]. Проблема 1 – это просто случай нулевого скрытого тепла (когда начальная температура равна нулю).
Наиболее удобный, общий и эффективный численный метод решения таких задач – это метод энтальпии [9], который приближает слабую постановку задачи (выражающую физику), известную как формулировка энтальпии. Это метод фиксированного домена, в котором только энтальпия (энергия) обновляется из закона сохранения, и она определяет фазу и неявная схема (итерации SOR и Ньютона), использующая решение Неймана для определения точности. В дальнейшем мы представим подобное сравнение со схемой супер временного степпинга.
Мы решаем общую энтальпийную постановку этих модельных задач численно на интервал 0 ⩽ x ⩽ 1 с использованием M = 100 равноотстоящих узлов. На задней грани x = 1 накладываем значения точного решения ((4) или решение Неймана) ((12) или решение Неймана), само оценивание при x = 1 в любое желаемое время. Таким образом, мы численно решаем одни и те же задачи, находим точные решения, и мы можем найти ошибку в численных решениях прямым сравнением с точными решениями. Граничные условия Дирихле ограничивают шаг по времени явной схемы по Δtexpl + Δx2 /3.
Схемы применимы к общим задачам проводимости / диффузии с непостоянным (даже зависящие от u) коэффициенты, т. е. они не настраиваются или не оптимизируются в каком-либо смысле для здесь рассматриваются простые задачи.
Мы дискретизируем уравнение в частных производных с помощью (интегрированных) конечных разностей и сравниваем производительность явной схемы супер-шага времени с полностью неявной и / или схема Кранка-Николсона с итерациями SOR и с итерациями Ньютона (с использованием прямого трехдиагонального решателя для шага Ньютона).
В явной схеме STS мы меняем N и v, тогда как в неявных схемах мы увеличиваем временной шаг Δt, кратный явному временному шагу texpl + Δx2 /3, устанавливая Δt = factor × Δtexpl с коэффициентом factor = 10,20,40, . . . Параметр экстраполяции SOR w находится из линейной теории SOR для уравнение теплопроводности и пробным путем для задачи Стефана, поскольку линейная теория там неприменима. Мы сообщаем значение w, которое минимизирует количество итераций.
Для определения точности каждой схемы мы проводим большое количество прямых сравнений с точным решением. Как отмечалось ранее, нельзя сравнивать чаще, чем N. Мы старались подобрать частоту сравнений так , чтобы общее количество сравнений (третий столбец таблиц) будет примерно одинаковым на всех схемах. В таблицах I и II дополнительно значениям параметров N, v или фактора, ω, мы сообщаем следующие величины для каждого запуска:
cmps = количество сравнений с точным решением
Emax = максимальная погрешность измерения температуры в фиксированных точках:
0; 0, 1;. . . ; 0,9 ;1 (линейно интерполировано по узловым значениям) по всем сравнениям (вычислено с помощью интегрирования трапецеидального правила) (определено только для задачи Стефана)
EL1 = максимальная L1-ошибка температуры в узлах по всем сравнениям
Efront = максимальная ошибка положения фронта расплава по всем сравнениям
s-шаги = количество cупершагов в СТС схеме
t-шаги = общее количество временных шагов
iters = количество выполненных итераций
Таблица I. Производительность STS и неявных схем по уравнению теплопроводности в течение 0 ⩽ x ⩽ , с M = 100 узлов
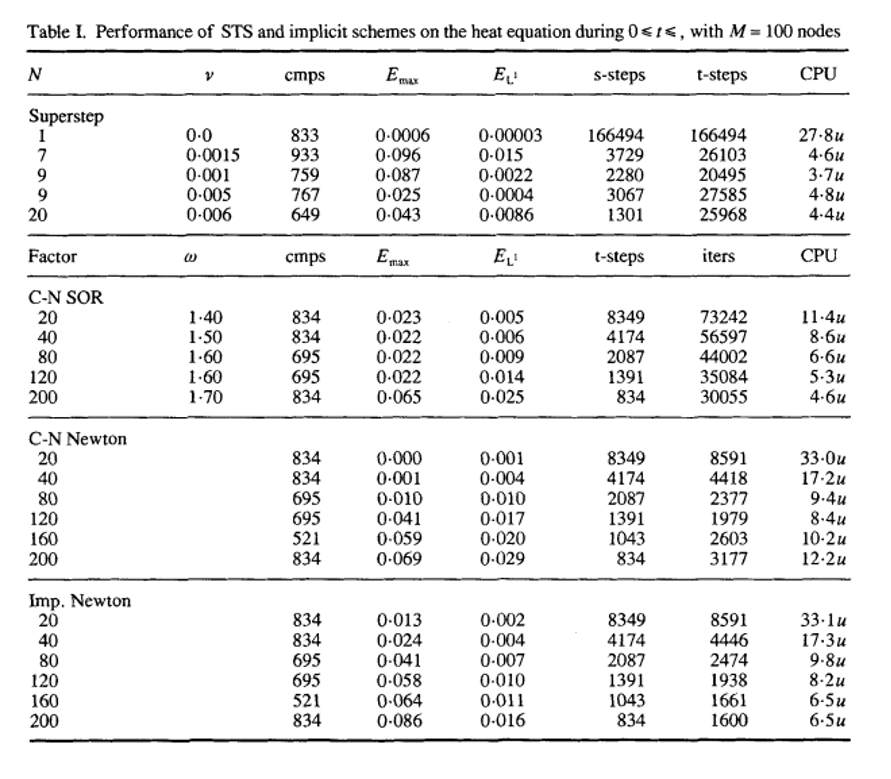
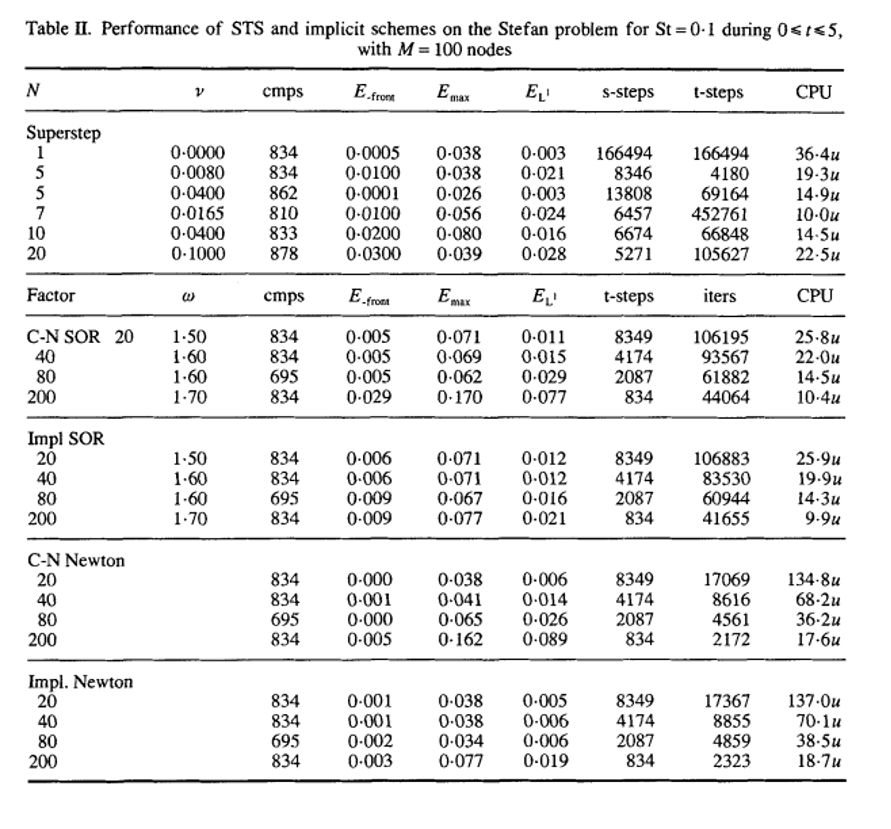
Таблица II. Выполнение STS и неявных схем в задаче Стефана для St = 0,1. в течение 0 ⩽ x ⩽5 , с M = 100 узлов.
Итерации неявных схем соответствуют временным шагам от явной схемы, поэтому они указаны в том же столбце. Мы использовали допуск для сходимости в итерационных схемах.
Поскольку температурный диапазон является нормированной на 0 ⩽ u ⩽1 , а также 0 ⩽ x ⩽ 1, обнаруженные ошибки можно рассматривать как процентные ошибки.
При увеличении ΔT ошибка растёт, и считается что работает с обеими ошибками меньше , чем примерно 6% . Расчёты выполнены с одинарной точностью на рабочей станции SUN Sparc 10 Model 40 , и мы записываем единицы ЦП (время пользователя), сообщаемые командой времени UNIX .
Исходя из сетевой UNIX-машины, это довольно ненадёжное число, но вместе с тем с общим количеством временных шагов или итераций это полезный показатель эффективности. Обратите внимание, что при N = 1, v = 0 – это есть сама стандартная явная схема.
Наилучшая производительность STS для этой задачи была достигнута для N = 9, v = O.OO1; Это интегрировало PDE в желаемое время всего за 20495 интервалов времени (по сравнению с 166494 Среди неявных схем Crank-Nicolson / SOR с Δt = 200 x Δtexpl была самой быстрой (30055 итераций).
С итерациями Ньютона было выполнено гораздо меньше итераций, но каждая итерация Ньютона
настолько дороже, что эффективность значительно страдает, и фактически она ухудшилась до коэффициента > 120. При большом Δt (т.е. коэффициент > 120) итерации Ньютона на полностью неявном (обратном Euler) схема сделала лучше , чем на кривошипном-Николсона, но он по- прежнему значительно отстает от СТС в обоих по стоимости и точности.
Таблица II показывает аналогичные сравнения по задаче Стефана. Помимо поточных и L1 ошибок по температуре, мы показываем ошибку в расположении интерфейса Efront, снова обнаруженную по сравнению с точным (Нейманновским) решением. Фазовый переход устраняет эту проблему линейно и значительно ухудшает работу всех схем.
Лучшее исполнение STS в настоящее время является для N = 5, v = 0,008; это уменьшило 166494 шага стандартной явной схемы до 41801 шага, ускорение в 4 раза. Опять же, увеличивая параметр v до 0,04, ошибки становятся меньше, чем даже у самой явной схемы, при приличном ускорении в 2,4 раза.
Схема Кранка-Николсона с итерациями SOR или Ньютона показывает неприемлемо большие ошибки для больших Δt. С другой стороны, полностью неявная схема / SOR становится конкурентоспособной с STS при коэффициенте = 200, при котором он достигает тех же ошибок фронта и L1, но его температура –
ошибка (Emax) в три раза больше, чем у STS. Итерации Ньютона снова оказались слишком дорогими.
При тех же затратах наиболее эффективной неявной схемой является полностью неявная / SOR при коэффициенте = 80, но его погрешности значительно хуже.
- ВЫВОДЫ
В статье описывается простой метод, который стабилизирует и ускоряет явную (прямую Эйлера) схему для параболических задач. Этот метод представляет собой вариант супер-шага по времени Генча схемы, и она принадлежит к классу методов Рунге-Кутта-Чебышева.
Представленные анализ и расчёты показывают, что супер-пошаговый режим не только очень полезен и прост в реализации в существующем явном коде, но при этом впечатляюще эффективен. Он работает как минимум так же быстро, он обеспечивает сопоставимую или лучшую точность, и, конечно же, его намного проще программировать (и для распараллеливания, для распределенных вычислений), чем стандартные неявные схемы для параболических проблемы.
Следует отметить, что STS не зависит от размерности пространства, поэтому он применяется также и в высшие измерения. Учитывая возросшую сложность и стоимость неявного многомерного схем, СТС там даже эффективнее.
БЛАГОДАРНОСТИ
Мы благодарны Стиву Кэмпбеллу и рецензентам за несколько замечаний, которые привели к лучшей
презентации этой статьи. Первого автора частично поддержал Science Alliance, центр программы передового опыта штата Теннесси. Третий автор был частично поддержан Управлением армейских исследований через грант № DAAJ304-91-1-0419, а также через Институт суперкомпьютеров Minesota во время пребывания в школе Университета Миннесоты.
CСЫЛКИ
- I.П.Дж. ван дер Хоувен, Построение формул интегрирования для начальных задач, NorthHolland, 1977 год.
- ВерверДж. Г., Хндсдорфер У., Сомейджер Б. П. , «Свойства сходимости уравнений Рунге-Кутта-
Метод Чебышева ‘, Numer. Math., 57, 157-178 (1900).
- Р.С.Варга, Матричный итерационный анализ, Prentice-Hall, 1962.
- W. Gentzsch, A. Schluter, «Об одношаговых методах с циклическим изменением размера шага для решения параболических дифференциальные уравнения (немецкий),2. Angew, Math. Мех., 58, Т415-Т416 (1978).
- П.Дж. ван дер Хоувен, Построение формул интегрирования для начальных задач, NorthHolland, 1977 год.
- ГентчВ. «Численное решение линейных и нелинейных параболических дифференциальных уравнений по времени. Дискретизация третьего порядка точности », в EH Hirschel (Ed.), Proceedings of the Third GAMM- Conference on Numerical Methods in Fluid Mechanics, Friedr. Vieweg & Sohn, 1979, стр. 109-117.
- Ж.-Ж.Дру, ‘Трехмерное численное моделирование затвердевания с помощью улучшенной явной схемы ‘, Comput. Methods Appl. Mech. Eng., 85, 57-74 (1991).
- В. Маркофф, «Uber Polynome, die in einem gegebenen Interval1 moglichst wenig von Null abweichen»,
Ann., 77, 213-258 (1892) (перевод и сжатие Дж. Гроссмана опубликованной на русском языке статьи в 1892 г.)).
- АлексиадесВ., Соломон А. Д. Математическое моделирование процессов плавления и замораживания. Hemisphere hbl. Hemisphere hbl. Co., Washington DC, 1993