Тропічна інтерполяція
Френк Соттіл
9 жовтня 2004, Коледж Стейшн, Техас.
![]() Стаття за осінній випуск 2004 р. «Емісар », інформаційний бюлетень ІГРН. ArXiv.org/math/0501146 .
Стаття за осінній випуск 2004 р. «Емісар », інформаційний бюлетень ІГРН. ArXiv.org/math/0501146 .
Усім відомо, що дві точки визначають пряму, а багато людей, які вивчали геометрію, знають, що п’ять точок на площині визначають конус. Загалом, якщо у вас є m випадкових точок на площині, і ви хочете провести через всі їх раціональну криву ступеня d , може не бути рішення цієї проблеми інтерполяції (якщо m занадто велике), або нескінченна кількість розв’язків (якщо m занадто мале) або кінцевої кількості рішень (якщо m правильне). Виявляється, що ” m якраз” означає m =3 d -1 ( m =2 для прямих і m =5 для конусів).
Складніше питання: якщо m =3 d -1, скільки раціональних кривих ступеня d інтерполюють точки? Назвемо це число N d , щоб N 1 =1 і N 2 =1, оскільки пряма і конус попереднього абзацу єдині. Давно відомо, що N 3 =12, а в 1873 році Zeuthen [ Ze ] показав, що N 4 =620. Так стояла справа приблизно десять років тому, коли Концевич і Манін [ К.М. ] використовували асоціативність у квантовій когомології, щоб дати елегантну рекурсію для цього числа.
Теми дослідження в зимовому семестрі MSRI 2004 року з топологічних аспектів реальної алгебраїчної геометрії включали перерахувальну реальну алгебраїчну геометрію, тропічну геометрію, реальні плоскі криві та застосування реальної алгебраїчної геометрії. Усі вони сплетені разом у розгорнутій історії цієї проблеми інтерполяції, прототипової проблеми перелічної геометрії , яка є мистецтвом підрахунку геометричних фігур, визначених заданими умовами випадковості. Ось ще одна проблема: скільки прямих у просторі зустрічаються з чотирма даними прямими? Щоб відповісти на це запитання, зверніть увагу, що три лінії лежать на унікальному гіперболоїді з двома лінійками.
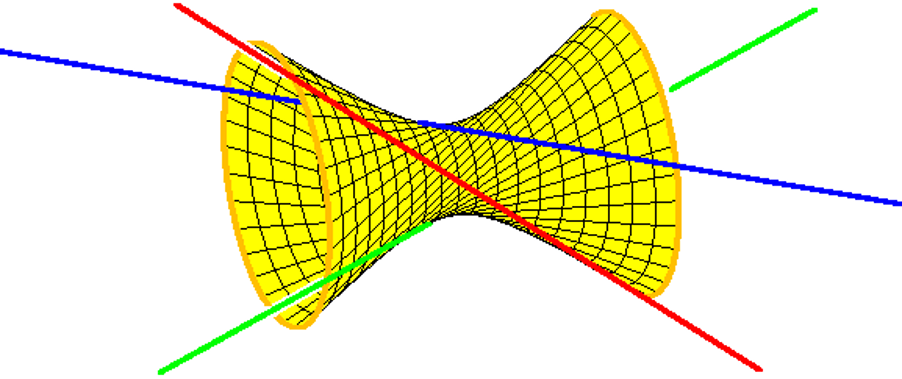
Три рядки лежать в одній лінійці, а друга лінійка складається з рядків, що зустрічаються з цими трьома рядками. Оскільки гіперболоїд визначається квадратним рівнянням, четверта лінія перетинатиметься з ним у двох точках. Через кожну з цих двох точок проходить пряма у другій лінійці, і це дві прямі, що перетинаються нашими чотирма заданими прямими.
Перелічна геометрія найкраще працює над комплексними числами, оскільки кількість дійсних фігур досить тонко залежить від конфігурації фігур, що дає умови виникнення. Наприклад, четверта лінія може зустрічатися з гіперболоїдом у двох дійсних точках або в двох комплексно спряжених точках, і тому існує дві або жодної з дійсних прямих, які відповідають усім чотирьом. Виходячи з багатьох прикладів, ми прийшли до висновку, що будь-яка перелічувальна проблема може мати всі її рішення бути реальними [ Отже ].
Іншою такою проблемою є 12 раціональних кривих, що інтерполюють 8 точок на площині. Більшість математиків знайомі з вузловою (раціональною) кубікою, показаною зліва нижче. Є ще один тип реального раціонального куба, показаний праворуч.
 |
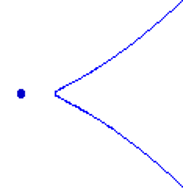 |
На другій кривій дві комплексно-спряжені гілки зустрічаються в ізольованій точці. Якщо ми нехай N ( t ) — кількість реальних кривих типу t , що інтерполюють 8 заданих точок, то Харламов і Дегтярьов [ Д.К. ] показали, що
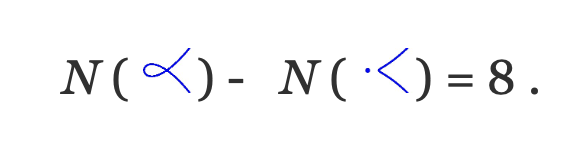
Ось опис їх елементарних топологічних методів.
Оскільки таких кривих не більше 12,
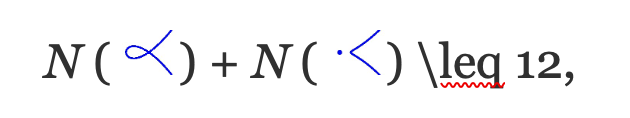
тож існує 8, 10 або 12 реальних раціональних кубиків, що інтерполюють 8 дійсних точок на площині, залежно від числа (0, 1, або 2) з кубиків із ізольованою точкою. Таким чином, буде 12 реальних раціональних кубиків, які інтерполюють будь-які 8 з 9 точок перетину двох кубиків нижче.
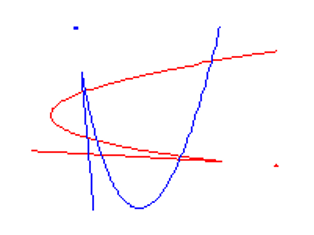
Велшингер [ W ], який був постдоком MSRI минулої зими, розвинув цей приклад у теорію. Загалом, особливістю реальної раціональної плоскої кривої C є вузли або ізольовані точки. Парність кількості вузлів є його знаком s ( C ), який дорівнює або 1, або -1. За 3 d -1 реальних точок на площині Вельшингер вважав абсолютне значення величини
s ( C ),
сума за всіма реальними раціональними кривими C ступеня d , які інтерполюють точки. Він показав, що ця зважена сума не залежить від вибору балів. Запишіть W d для цього інваріанта Вельшингера. Наприклад, ми щойно побачили, що W 3 =8.
Це було проривом, оскільки W d був (майже) першим справді нетривіальним інваріантом у перерахунковій реальній алгебраїчній геометрії. Зверніть увагу, що W d є нижньою межею для числа реальних раціональних кривих через 3 d -1 реальних точок на площині, а W d \leq N d .
Михалкін, який був організатором семестру, надав ключ до обчислення W d за допомогою тропічної алгебраїчної геометрії [ Mi ]. Це геометрія тропічного півкільця, де операції max і + над дійсними числами замінюють звичайні операції + і множення. Тропічний поліном — це кусково-лінійна функція виду
T ( x , y ) = max ( i , j ) { x i + y j + c i , j } ,
де обчислення ведеться за допомогою звичайних арифметичних операцій і максимум береться для кінцевої підмножини Z 2 показників T і c i , j – коефіцієнти реального числа T . Тропічний поліном T визначає тропічну криву, яка є множиною точок ( x , y ), де T ( x , y ) не є диференційованим. Ось кілька тропічних кривих.
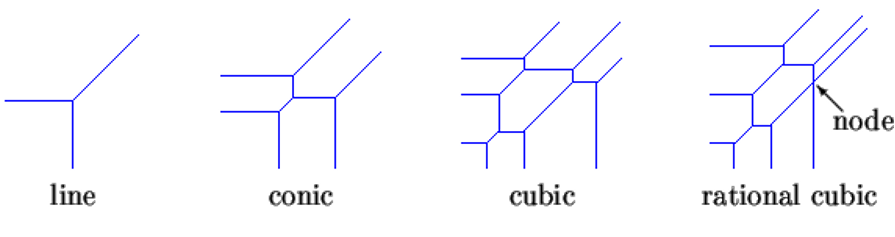
Ступінь тропічної кривої — це кількість променів, що мають тенденцію до нескінченності в будь-якому з трьох напрямків на захід, південь або північний схід. Тропічна крива є раціональною, якщо це кусково-лінійне занурення дерева. Вузли мають валентність 4.
Михалкін показав, що існує лише скінченна кількість раціональних тропічних кривих ступеня d , що інтерполюють 3 d -1 загальних точок. Хоча кількість таких кривих залежить від вибору точок, Михалкін прикріпив позитивні кратності до кожної тропічної кривої, так що зважена сума не відповідає, а насправді дорівнює N d . Він також звів ці кратності та перерахування тропічних кривих до комбінаторики ґраткових шляхів у трикутнику із довжиною сторони d .
Михалкін використовував відповідність, що включає карту Log : ( C * ) 2 –> R 2 , визначену ( x , y )|–>(log| x |,log| y |), і певну `велику комплексну межу’ комплексної структури на ( C * ) 2 . За цієї великої комплексної межі раціональні криві ступеня d , що інтерполюють 3 d -1 точки в ( C * ) 2 , деформуються до “складних тропічних кривих”, зображення яких під Log є звичайними тропічними кривими, що інтерполюють зображення точок. Кратність тропічної кривої T– кількість складних тропічних кривих, які проектуються на T .
А як щодо справжніх кривих? Дотримуючись цієї відповідності, Михалкін приєднав реальну кратність до кожної тропічної кривої і показав, що якщо тропічні криві, що інтерполюють задані 3 d -1 точки, мають повну реальну кратність N , то є 3 d -1 реальні точки, які інтерполюють N реальних раціональних кривих ступеня d . Ця реальна множинність знову виражається в термінах ґраткових шляхів.
А як щодо інваріанта Вельшингера? Таким же чином Михалкін прикріпив вагу зі знаком до кожної тропічної кривої (тропічний варіант знака Вельшингера) і показав, що відповідна зважена сума дорівнює інваріанту Вельшингера. Як і раніше, ця тропічна вага зі знаком може бути виражена в термінах решітки.
Протягом семестру в MSRI Ітенберг, Харламов і Шустін [ ІКС ] використовували результати Михалкіна для оцінки інваріанта Вельшингера. Вони показали, що W d \geq d !/3, а також
log W d = log N d + O ( d ), log N d = 3 d log d + O ( d ) .
Таким чином, принаймні логарифмічно, більшість раціональних кривих ступеня d , що інтерполюють 3 d -1 реальних точок на площині, є реальними.
Існують ще два приклади цього явища нижніх меж, перший з яких передує роботі Вельшингера. Припустимо, що d парне і нехай W ( s ) — дійсний багаточлен ступеня k ( d – k +1). Потім Єременко та Габріелов [ Є.Г. ] показали, що існують дійсні поліноми f 1 ( s ),…, f k ( s ) ступеня d , визначник Вронського — W ( s ). Насправді вони довели нижню межу для числа k-набори поліномів з точністю до еквівалентності. Аналогічно, в MSRI, Сопрунова і я [ SS ] вивчали розріджені поліноміальні системи, пов’язані з множинами, показуючи, що кількість реальних рішень обмежена знизу дисбалансом знаків набору. Такі нижні межі для задач перерахування, які передбачають існування реальних рішень, важливі для додатків.
Наприклад, цю історію розповідали за пивом одного вечора на семінарі MSRI з геометричного моделювання та реальної алгебраїчної геометрії в квітні 2004 року. Учасник, Шичо, зрозумів, що результат W 3 =8 для кубиків пояснив, чому розроблений ним метод завжди здавався таким, що працює. Це був алгоритм для обчислення приблизної параметризації дуги кривої за допомогою реальної раціональної кубічної інтерполяції 8 точок на дузі. Залишилося знайти умови, які б гарантували існування вирішення, близького до дуги. Це щойно вирішив Фідлер-Ле Тузе, постдок MSRI, який вивчав кубіки (не обов’язково раціональні), інтерполюючи 8 точок, щоб допомогти класифікувати реальні плоскі криві ступеня 9.
Бібліографія
| [DK] | А. І. Дегтярьов, В. М. Харламов, Топологічні властивості дійсних алгебраїчних різновидів: шлях Рохліна , УМН. наук 55 (2000), вип. 4(334), 129–212. |
| [EG] | Єременко А., Габріелов А. Ступені дійсних відображень Вронського , Дискретне обчислення. Geom. 28 (2002), вип. 3, 331–347. |
| [IKS] | І. Ітенберг, В. Харламов, Е. Шустін, Логарифмічна еквівалентність інваріантів Вельшингера та Громова-Віттена , arXiv:math.AG/0407188 . |
| [KM] | М. Концевич та Ю. Манін, класи Громова-Віттена, квантові когомології та перелічна геометрія , Ком. Математика фіз. 164 (1994), вип. 3, 525–562. |
| [Mi] | Г. Михалкін, Перелічна тропічна алгебраїчна геометрія в R 2 , arXiv:math.AG/0312530 . |
| [СС] | Е. Сопрунова та Ф. Соттіле, Нижні межі для дійсних розв’язків розріджених поліноміальних систем , arXiv:math.AG/0409504 . |
| [So] | F. Sottile, Перелічна реальна алгебраїчна геометрія , Алгоритмічна та кількісна реальна алгебраїчна геометрія (Piscataway, NJ, 2001), DIMACS Ser. Дискретна математика. Теорет. Обчис. наук, вип. 60, амер. Математика Soc., Providence, RI, 2003, с. 139–179. |
| [W] | Ж.-Й. Вельшингер, Інваріанти дійсних раціональних симплектичних 4-много різновидів і нижні оцінки в реальній перелічувальній геометрії, C. R. Math. акад. наук. Париж 336 (2003), вип. 4, 341–344. |
| [Ze] | H. G. Zeuthen, Almindelige Egenskaber ved Systemer af plane Kurver , Danske Videnskabernes Selskabs Skrifter, Naturvidenskabelig og Mathematisk, Afd. 10 бд. IV (1873), 286–393. |
Ми вдячні нашому редактору Сільвіо Леві та членам MSRI, роботу яких ми описуємо.
За підтримки грантів Національного наукового фонду CAREER DMS-0134860 і DMS-9810361 (фінансування MSRI), а також Математичного інституту Клея.
Останнє оновлення: Пн, 23 квітня, 15:33:30 CEST 2018 року